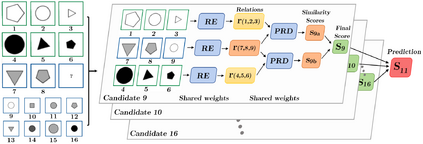
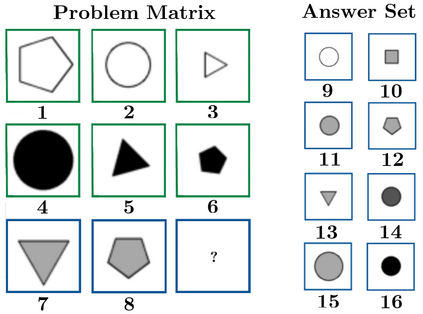
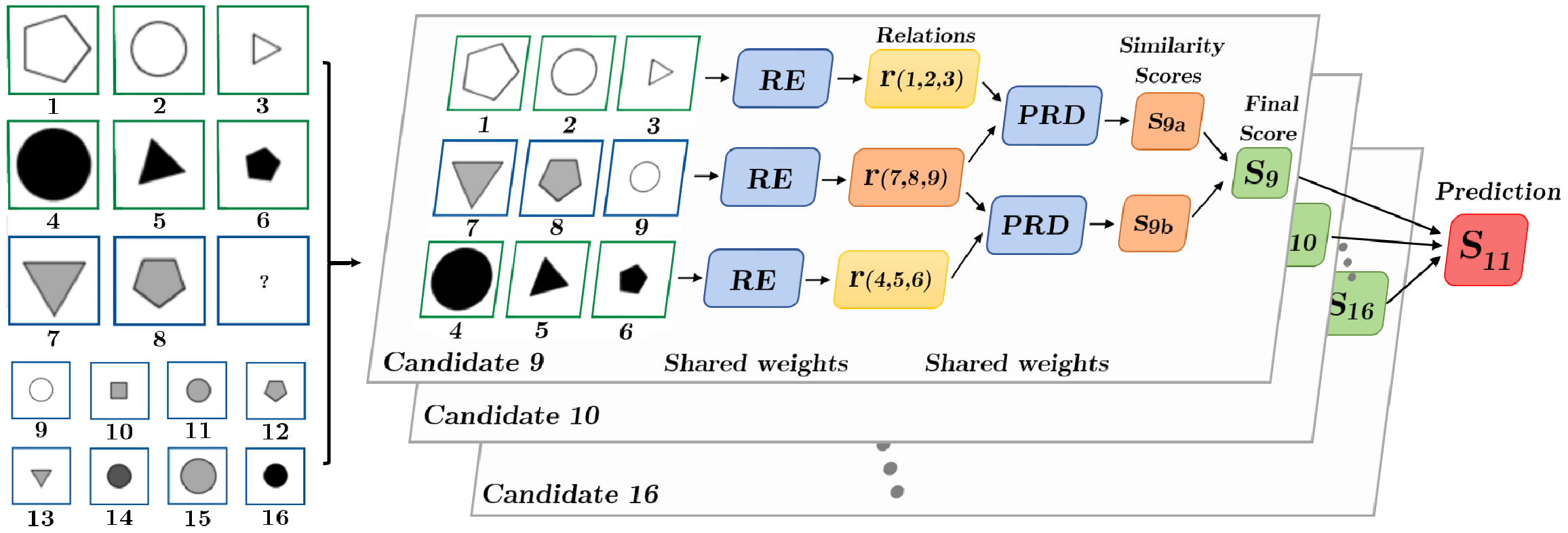
The ability to hypothesise, develop abstract concepts based on concrete observations and apply these hypotheses to justify future actions has been paramount in human development. An existing line of research in outfitting intelligent machines with abstract reasoning capabilities revolves around the Raven's Progressive Matrices (RPM). There have been many breakthroughs in supervised approaches to solving RPM in recent years. However, this process requires external assistance, and thus it cannot be claimed that machines have achieved reasoning ability comparable to humans. Namely, humans can solve RPM problems without supervision or prior experience once the RPM rule that relations can only exist row/column-wise is properly introduced. In this paper, we introduce a pairwise relations discriminator (PRD), a technique to develop unsupervised models with sufficient reasoning abilities to tackle an RPM problem. PRD reframes the RPM problem into a relation comparison task, which we can solve without requiring the labelling of the RPM problem. We can identify the optimal candidate by adapting the application of PRD to the RPM problem. Our approach, the PRD, establishes a new state-of-the-art unsupervised learning benchmark with an accuracy of 55.9% on the I-RAVEN, presenting a significant improvement and a step forward in equipping machines with abstract reasoning.
翻译:假设能力、根据具体观察发展抽象概念的能力以及运用这些假设来为今后的行动辩护的能力,在人类发展中是至高无上的。现有研究线是,在安装智能机器时,以抽象推理能力取代智能机器,围绕乌鸦的渐进式矩阵(RPM)进行。近年来,在有监督地解决RPM问题的方法上取得了许多突破。然而,这一过程需要外部援助,因此不能声称机器已经取得了与人类可比的推理能力。也就是说,一旦正确引入了RPM规则,即关系只能存在行/校,人类就可以不经监督或事先经验解决RPM问题。在本文中,我们引入了一种配对式关系歧视者(PRD),这是一种开发无监督的模型,有足够的推理能力解决RPM问题的技术。PRD将RP问题重新设计成一个比较任务,我们无需为RPM问题贴标签就可以解决这个问题。我们可以通过将PRD的应用适应于RPM问题来确定最佳人选。我们的方法,即PRD,在新的状态上建立一个无节制步骤的升级的升级标准,用55RPRD,并用一个重要推算的推算。