Recursive Rules with Aggregation: A Simple Unified Semantics

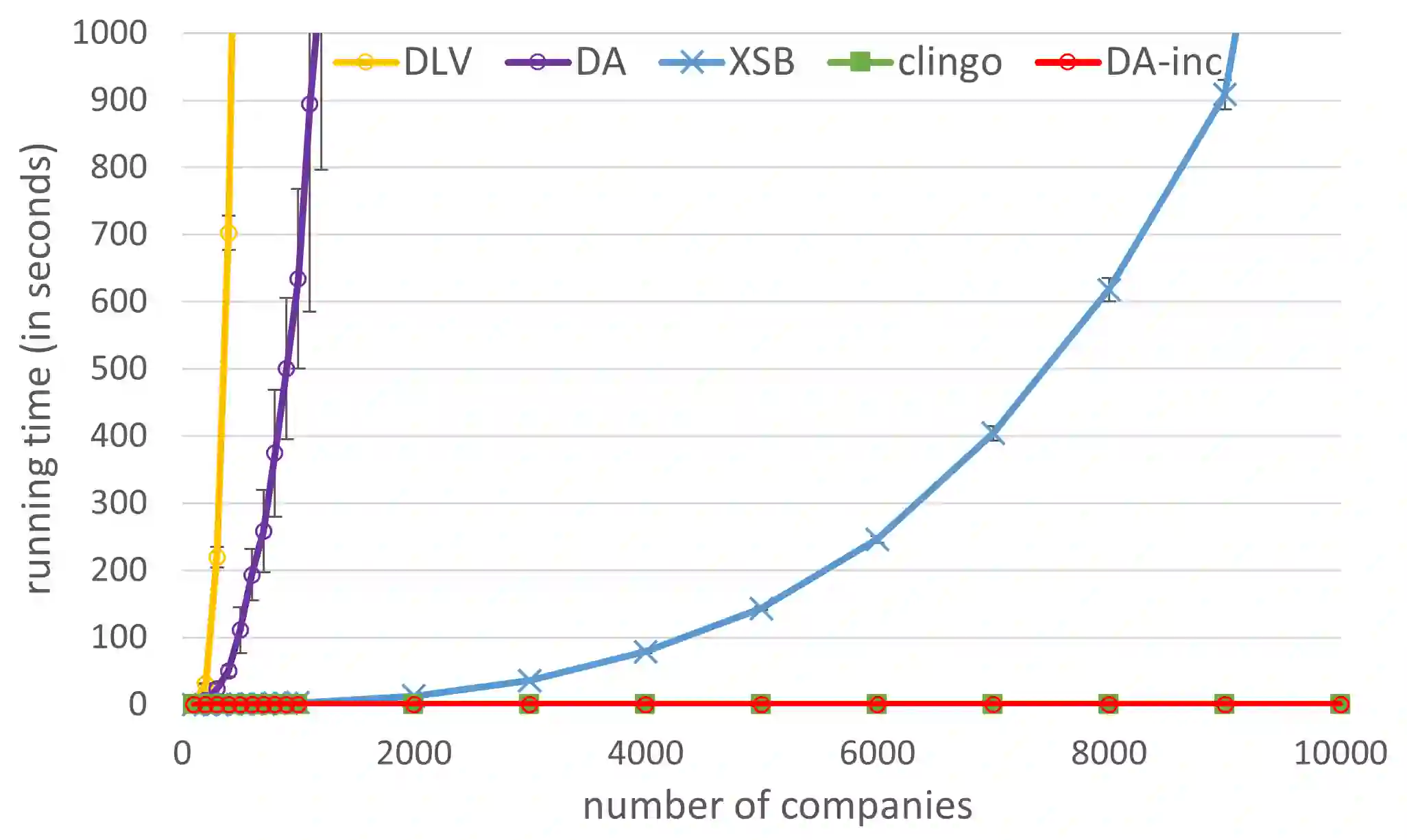
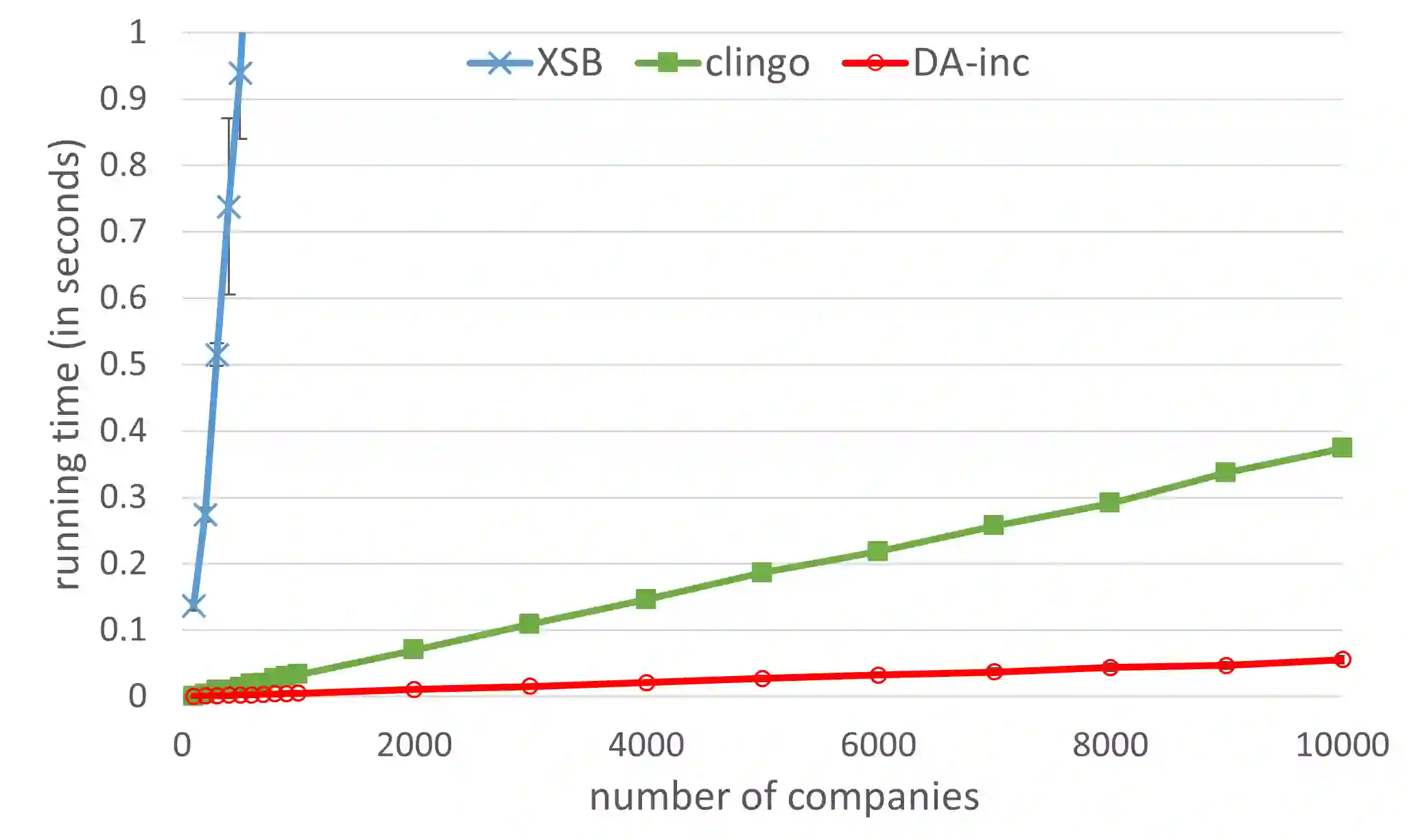
Complex reasoning problems are most clearly and easily specified using logical rules, but require recursive rules with aggregation such as counts and sums for practical applications. Unfortunately, the meaning of such rules has been a significant challenge, leading to many disagreeing semantics. This paper describes a unified semantics for recursive rules with aggregation, extending the unified founded semantics and constraint semantics for recursive rules with negation. The key idea is to support simple expression of the different assumptions underlying different semantics, and orthogonally interpret aggregation operations using their simple usual meaning. We present formal definition of the semantics, prove important properties of the semantics, and compare with prior semantics. Besides exact inference over aggregations, we present an efficient approximation that gives precise answers to all examples we have studied from the literature. We also apply our semantics to a wide range of challenging examples, and show that our semantics is simple and matches the desired results in all cases. Finally, we describe experiments on the most challenging examples, exhibiting unexpectedly superior performance over well-known systems when they can compute correct answers.