A nonstationary spatial covariance model for data on graphs

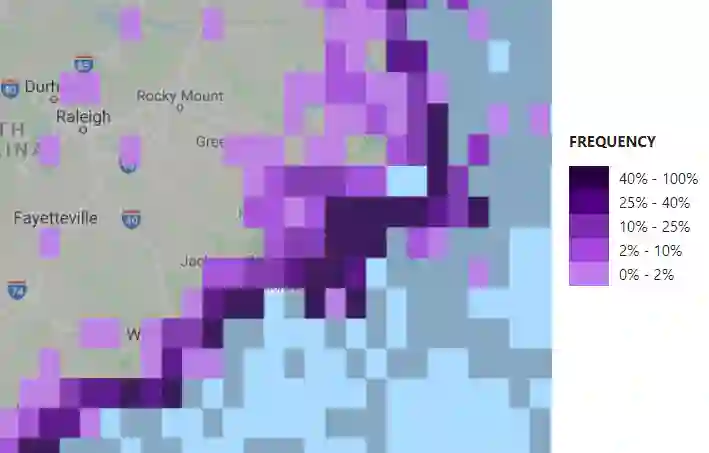
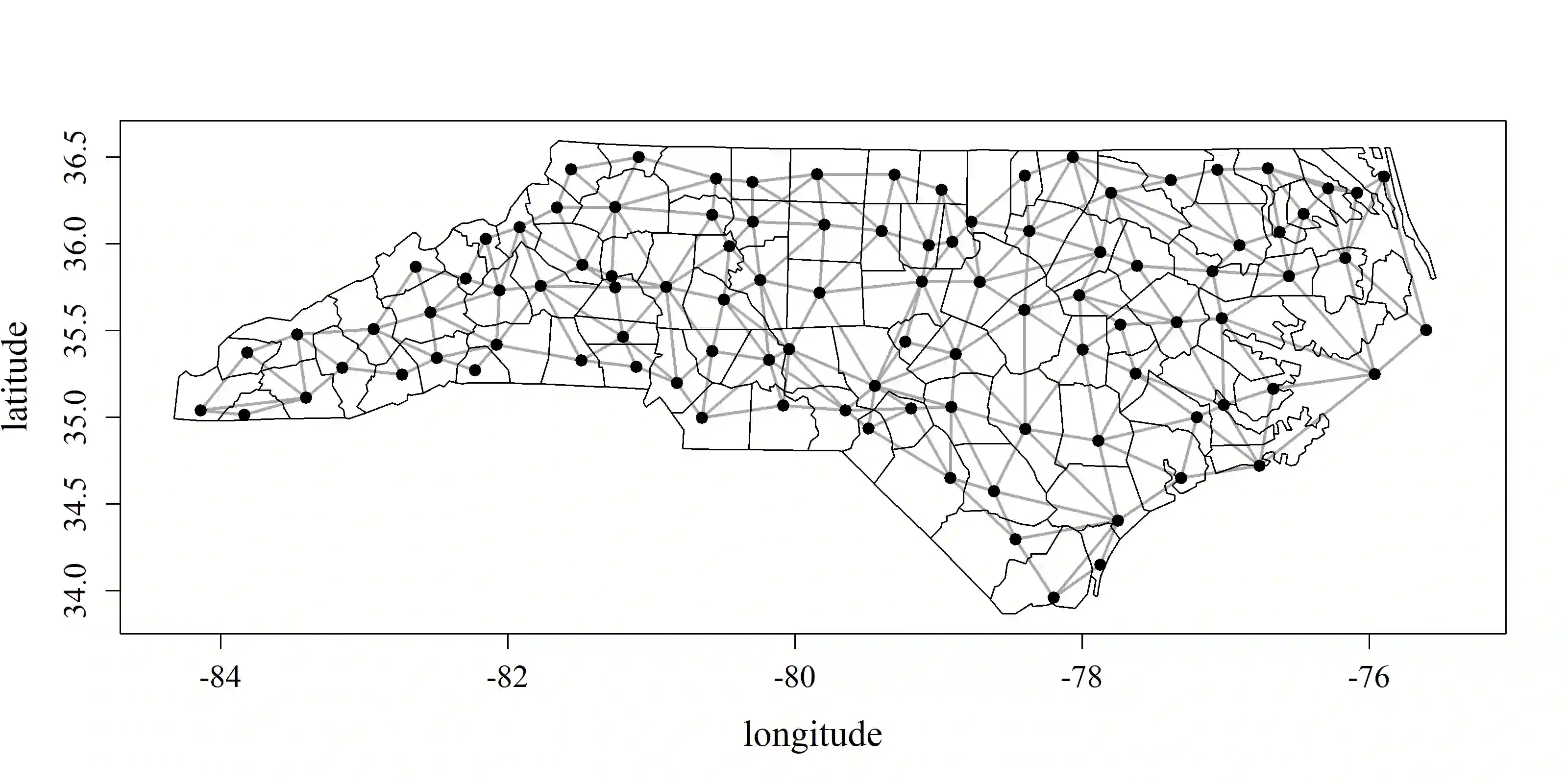
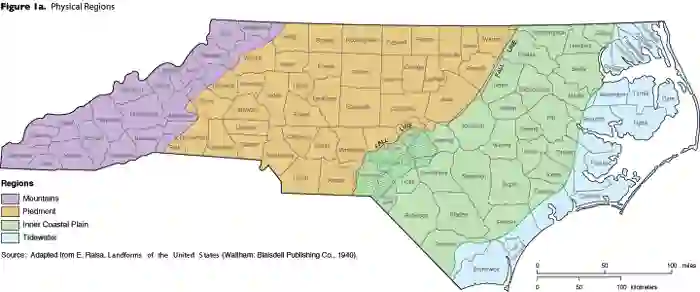
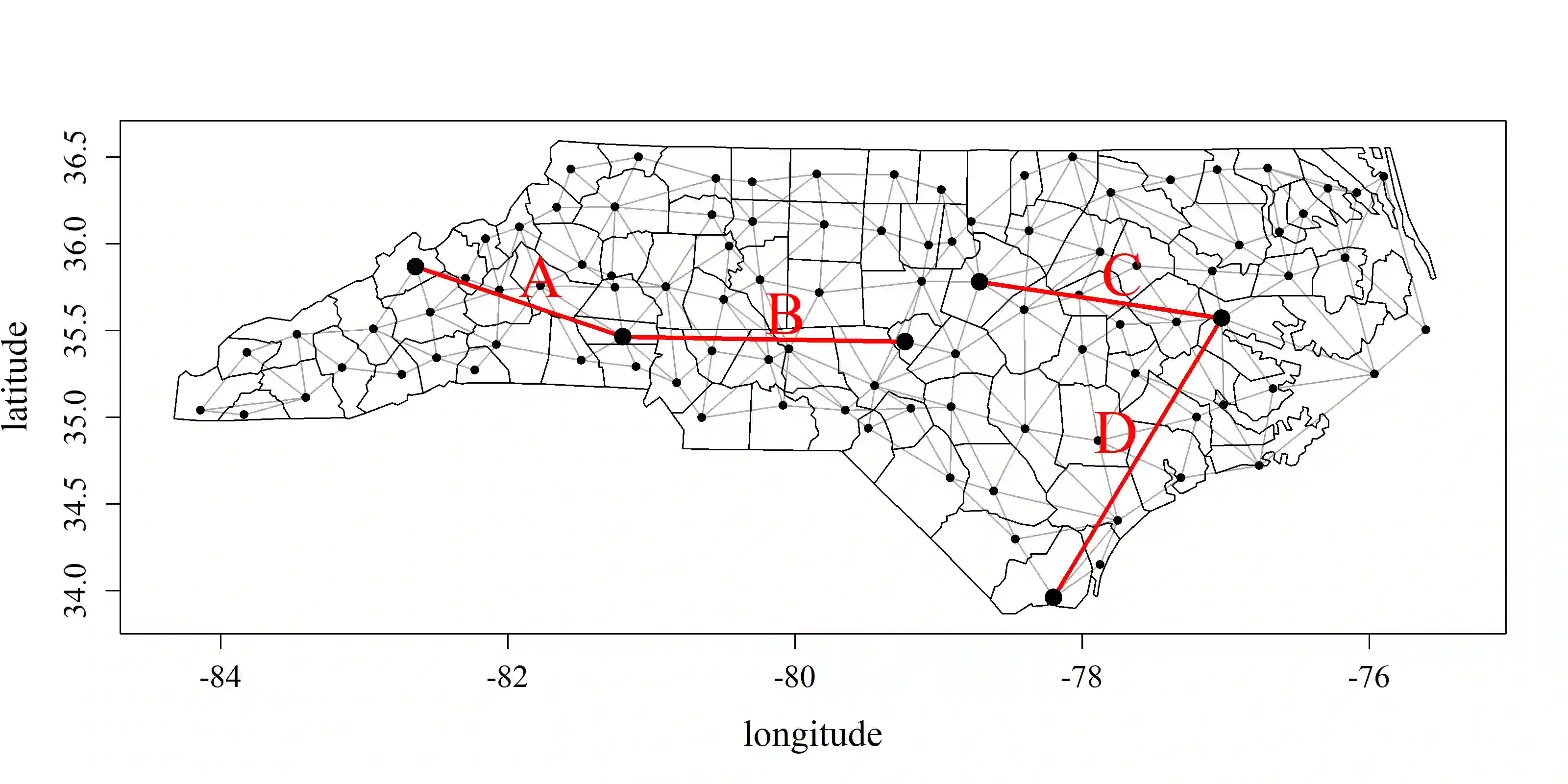
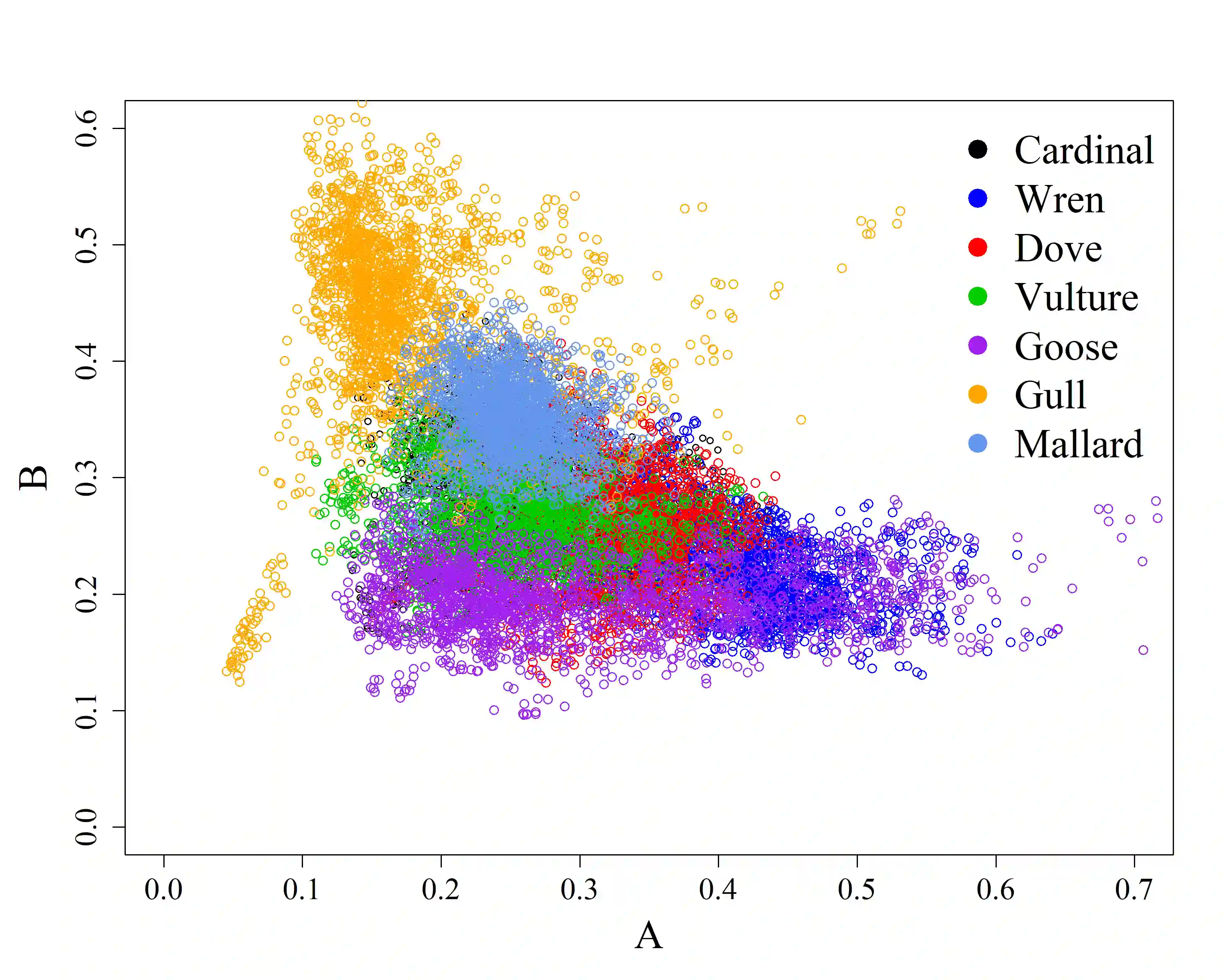
Spatial data can exhibit dependence structures more complicated than can be represented using models that rely on the traditional assumptions of stationarity and isotropy. Several statistical methods have been developed to relax these assumptions. One in particular, the "spatial deformation approach" defines a transformation from the geographic space in which data are observed, to a latent space in which stationarity and isotropy are assumed to hold. Taking inspiration from this class of models, we develop a new model for spatially dependent data observed on graphs. Our method implies an embedding of the graph into Euclidean space wherein the covariance can be modeled using traditional covariance functions such as those from the Mat\'{e}rn family. This is done via a class of graph metrics compatible with such covariance functions. By estimating the edge weights which underlie these metrics, we can recover the "intrinsic distance" between nodes of a graph. We compare our model to existing methods for spatially dependent graph data, primarily conditional autoregressive (CAR) models and their variants and illustrate the advantages our approach has over traditional methods. We fit our model and competitors to bird abundance data for several species in North Carolina. We find that our model fits the data best, and provides insight into the interaction between species-specific spatial distributions and geography.