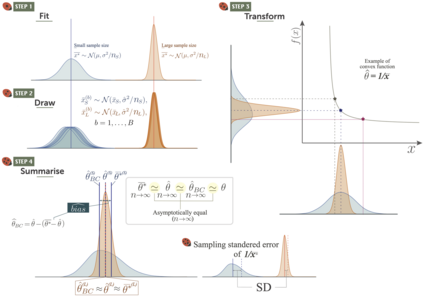
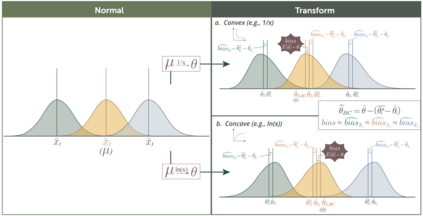
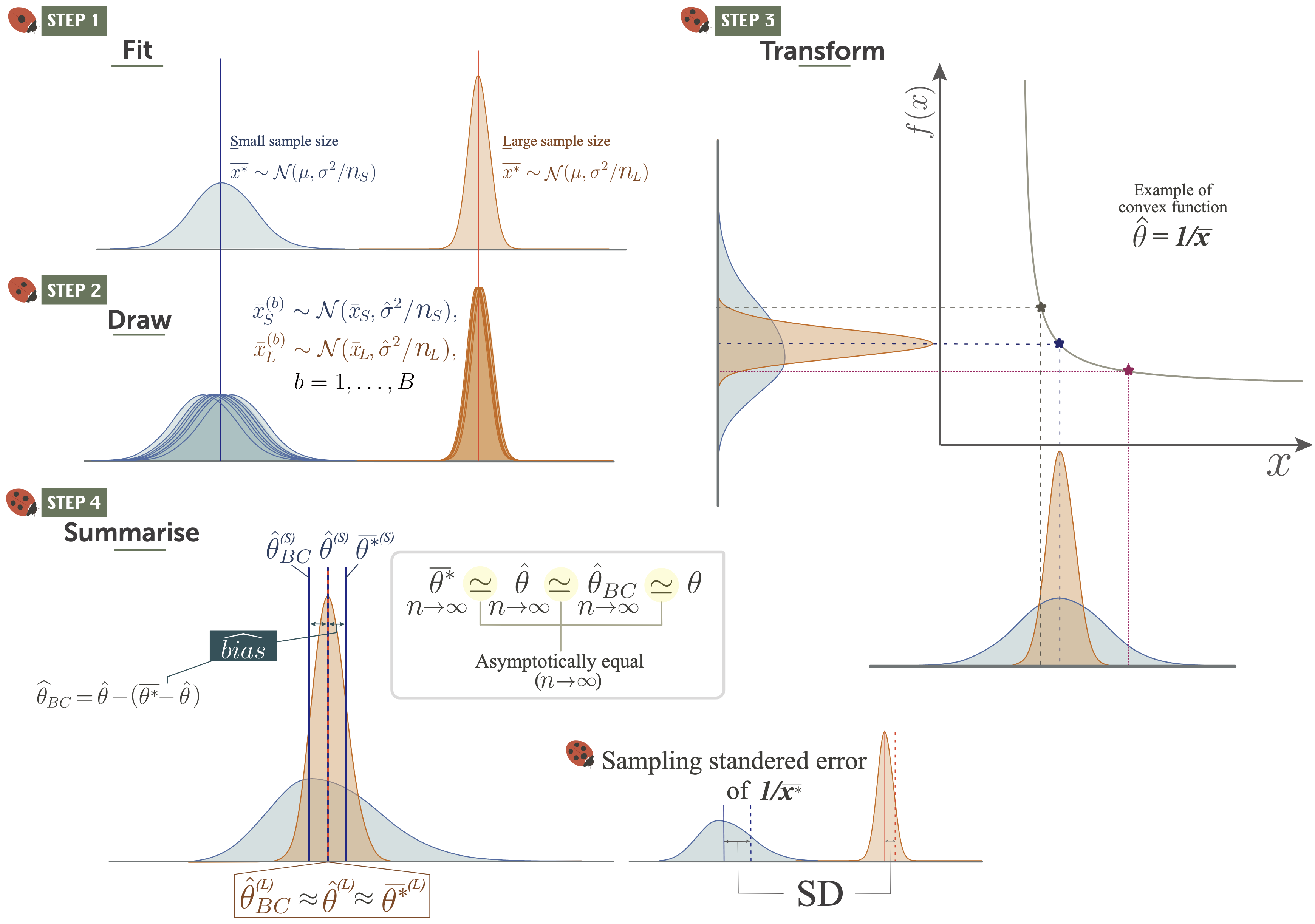
Meta-analyses require an effect-size estimate and its corresponding sampling variance from primary studies. In some cases, estimators for the sampling variance of a given effect size statistic may not exist, necessitating the derivation of a new formula for sampling variance. Traditionally, sampling variance formulas are obtained via hand-derived Taylor expansions (the delta method), though this procedure can be challenging for non-statisticians. Building on the idea of single-fit parametric resampling, we introduce SAFE bootstrap: a Single-fit, Accurate, Fast, and Easy simulation recipe that replaces potentially complex algebra with four intuitive steps: fit, draw, transform, and summarise. In a unified framework, the SAFE bootstrap yields bias-corrected point estimates and standard errors for any effect size statistic, regardless of whether the outcome is continuous or discrete. SAFE bootstrapping works by drawing once from a simple sampling model (normal, binomial, etc.), converting each replicate into any effect size of interest and then calculating the bias and sampling variance from simulated data. We demonstrate how to implement the SAFE bootstrap for a simple example first, and then for common effect sizes, such as the standardised mean difference and log odds ratio, as well as for less common effect sizes. With some additional coding, SAFE can also handle zero values and small sample sizes. Our tutorial, with R code supplements, should not only enhance understanding of sampling variance for effect sizes, but also serve as an introduction to the power of simulation-based methods for deriving any effect size with bias correction and its associated sampling variance.
翻译:暂无翻译