On the expressivity of bi-Lipschitz normalizing flows

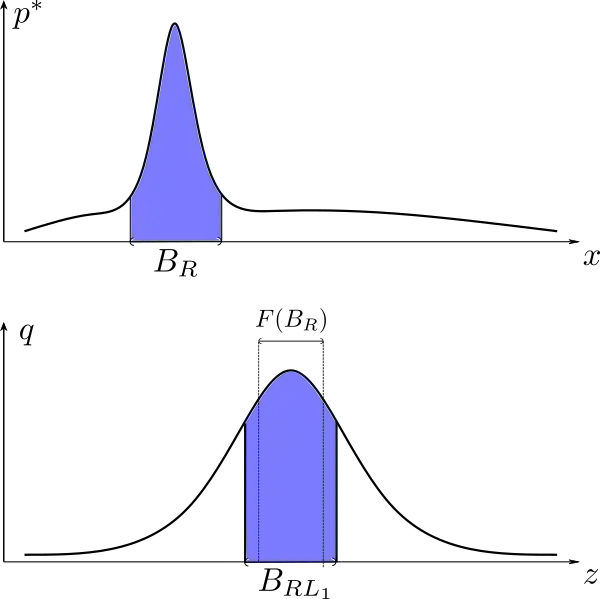
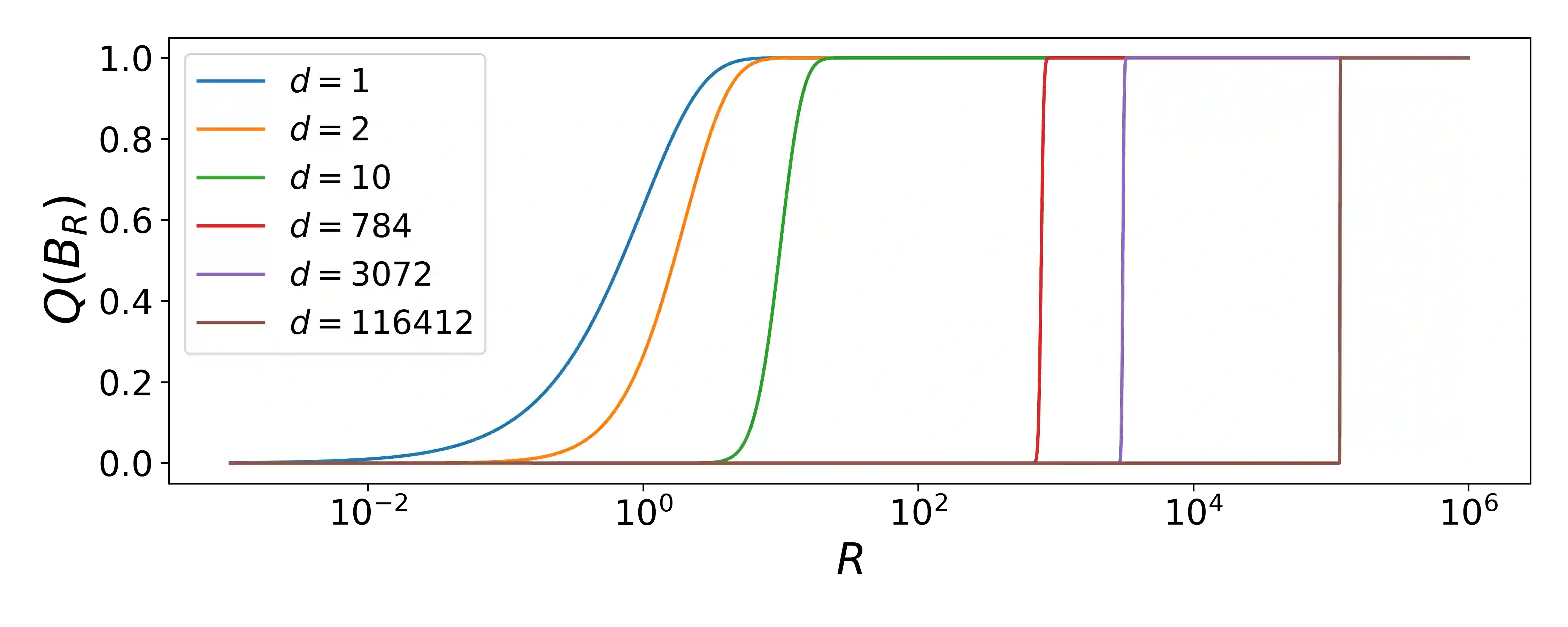
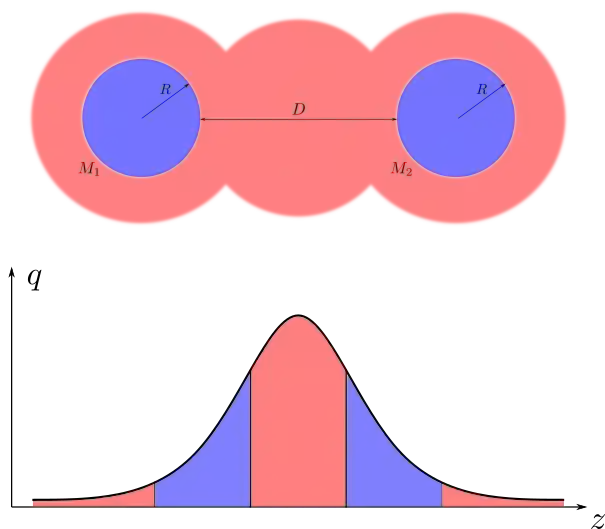
An invertible function is bi-Lipschitz if both the function and its inverse have bounded Lipschitz constants. Nowadays, most Normalizing Flows are bi-Lipschitz by design or by training to limit numerical errors (among other things). In this paper, we discuss the expressivity of bi-Lipschitz Normalizing Flows and identify several target distributions that are difficult to approximate using such models. Then, we characterize the expressivity of bi-Lipschitz Normalizing Flows by giving several lower bounds on the Total Variation distance between these particularly unfavorable distributions and their best possible approximation. Finally, we discuss potential remedies which include using more complex latent distributions.