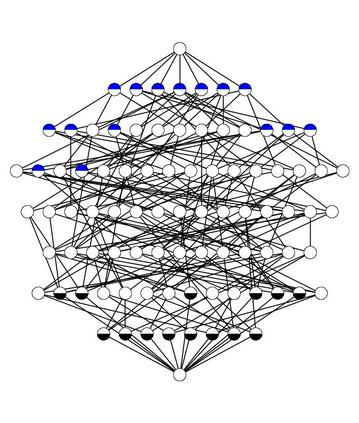
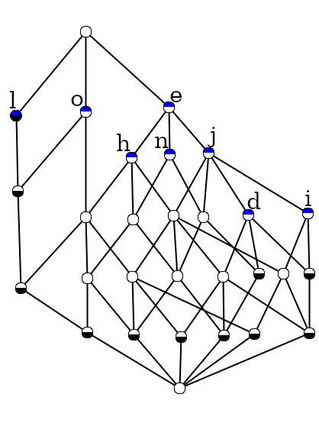
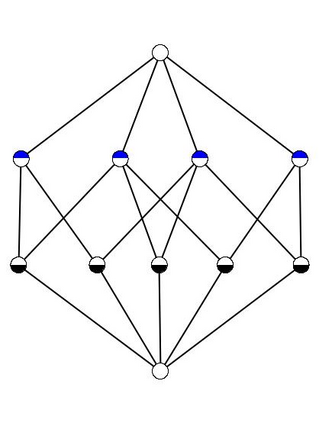
Formal Concept Analysis (FCA) allows to analyze binary data by deriving concepts and ordering them in lattices. One of the main goals of FCA is to enable humans to comprehend the information that is encapsulated in the data; however, the large size of concept lattices is a limiting factor for the feasibility of understanding the underlying structural properties. The size of such a lattice depends on the number of subcontexts in the corresponding formal context that are isomorphic to a contranominal scale of high dimension. In this work, we propose the algorithm ContraFinder that enables the computation of all contranominal scales of a given formal context. Leveraging this algorithm, we introduce delta-adjusting, a novel approach in order to decrease the number of contranominal scales in a formal context by the selection of an appropriate attribute subset. We demonstrate that delta-adjusting a context reduces the size of the hereby emerging sub-semilattice and that the implication set is restricted to meaningful implications. This is evaluated with respect to its associated knowledge by means of a classification task. Hence, our proposed technique strongly improves understandability while preserving important conceptual structures.
翻译:正式概念分析(FCA) 能够分析二进制数据,从概念中得出概念,并命令在固定空间中进行排序。 FCA的主要目标之一是使人类能够理解数据中包含的信息;然而,概念层的大小之大,是理解基本结构属性可行性的一个限制因素。这种结构层的大小取决于相应正式环境中与相对立的高度尺寸相异的子变量的数量。在这项工作中,我们提议了允许计算特定正式环境所有反向尺度的反向法比德尔法。利用这一算法,我们采用了三角调整法,一种新颖的方法,以便通过选择适当的属性子集,在正式环境中减少反向级尺度的数量。我们证明,三角调整一个环境会缩小新产生的子空间的大小,而其含义仅限于有意义的影响。我们通过分类任务对其相关知识进行评估。因此,我们采用三角调整法,通过选择一个适当的属性子集来大力改进概念结构,同时保持重要的理解性。