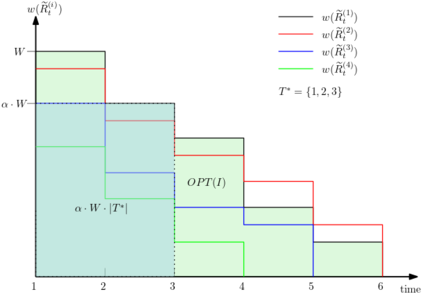
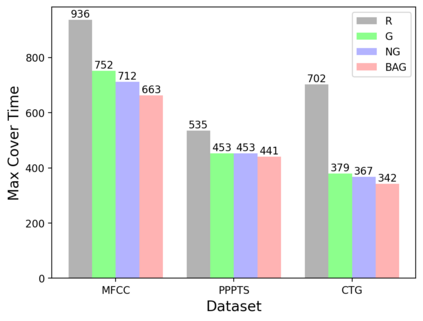
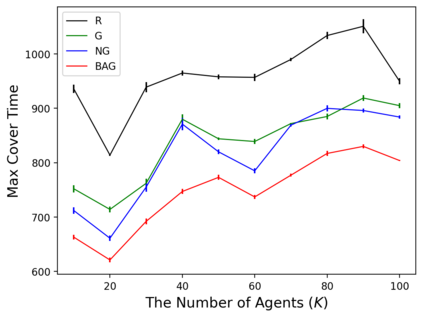
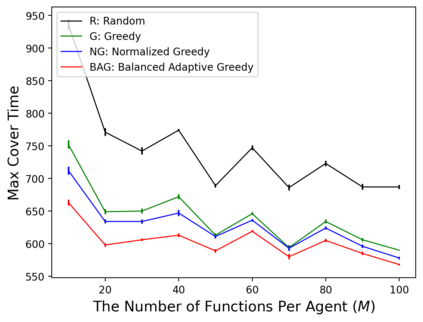
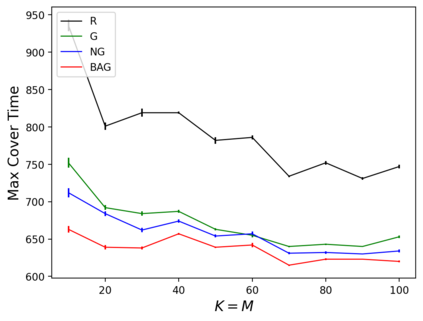
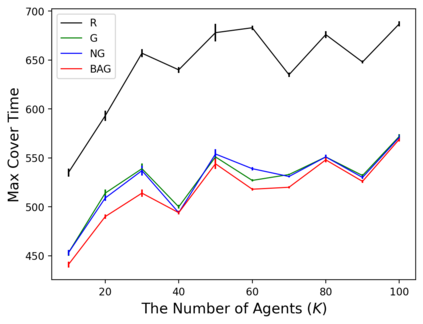
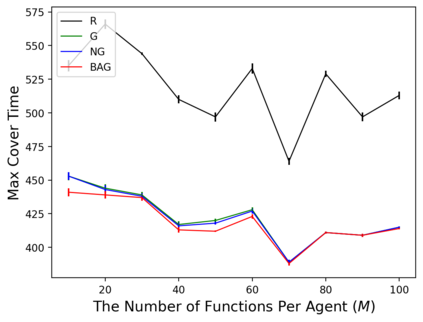
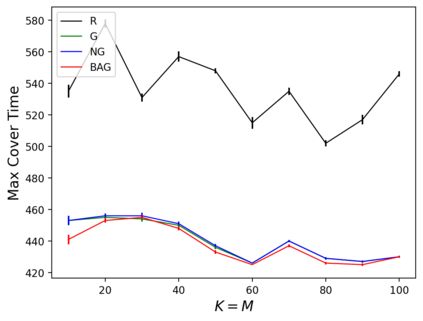
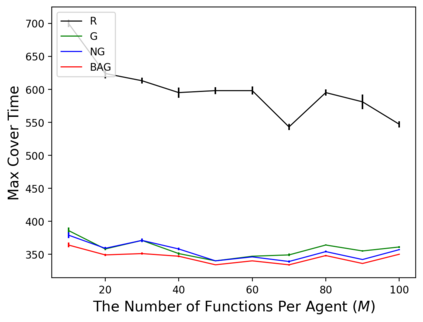
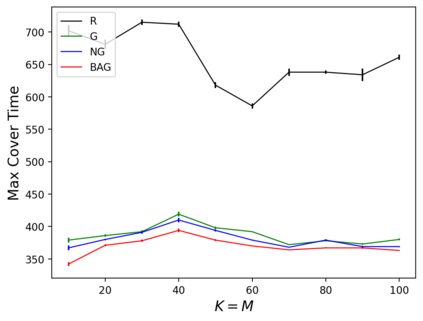
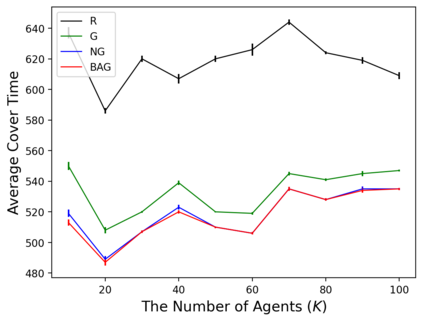
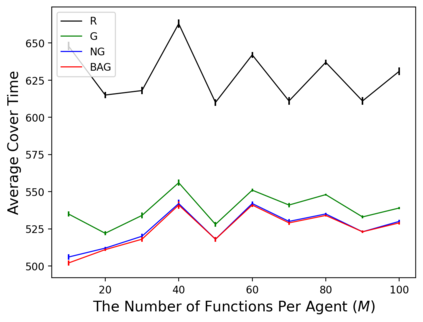
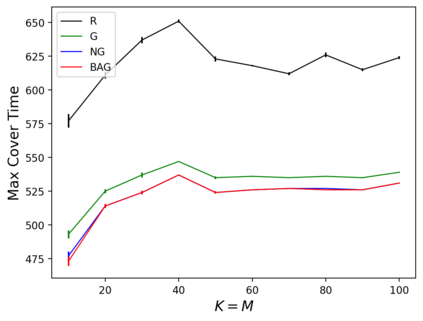
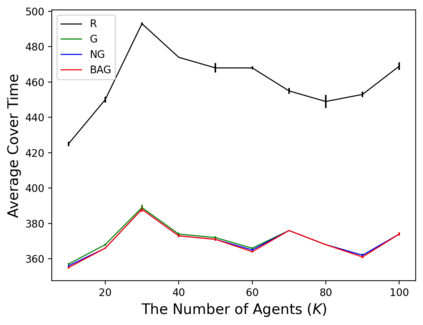
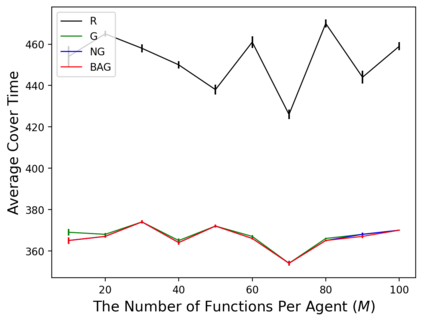
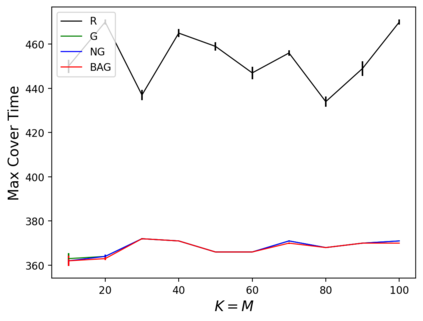
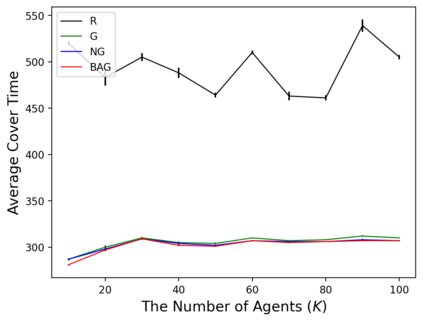
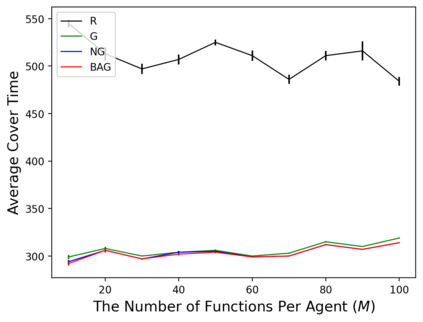
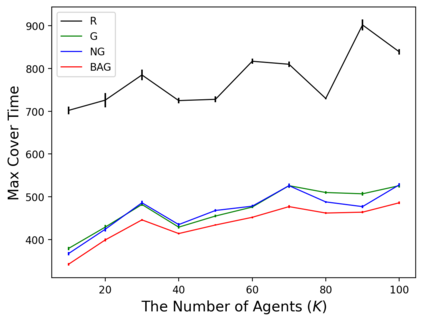
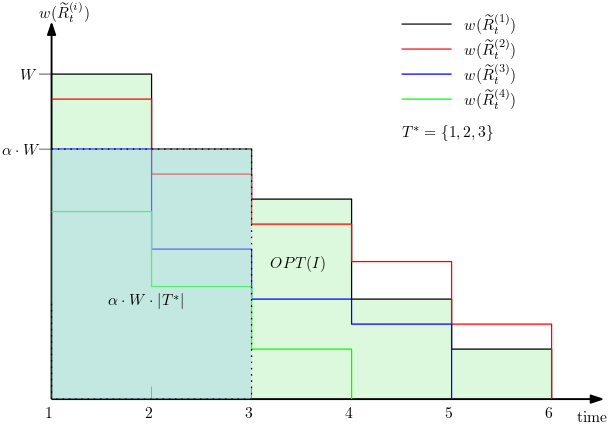
In the submodular ranking (SR) problem, the input consists of a set of submodular functions defined on a ground set of elements. The goal is to order elements for all the functions to have value above a certain threshold as soon on average as possible, assuming we choose one element per time. The problem is flexible enough to capture various applications in machine learning, including decision trees. This paper considers the min-max version of SR where multiple instances share the ground set. With the view of each instance being associated with an agent, the min-max problem is to order the common elements to minimize the maximum objective of all agents -- thus, finding a fair solution for all agents. We give approximation algorithms for this problem and demonstrate their effectiveness in the application of finding a decision tree for multiple agents.
翻译:在次模排序(SR)问题中,输入是由定义在元素总集上的一组次模函数组成。目标是为了使所有函数的值都在一个特定的阈值以上能够尽快地平均排列元素,假设我们每次选择一个元素。该问题足够灵活以涵盖机器学习中的各种应用,包括决策树。本文考虑SR的极小-极大版本,在该版本中,多个实例共享总集。将每个实例视为一个智能体,极小-极大问题就是为了对公共元素进行排序,以使所有智能体的最大目标最小 - 因此,为所有智能体寻找公平的解决方案。我们为此问题提供了近似算法,并在多个智能体寻找决策树的应用中证明了其有效性。