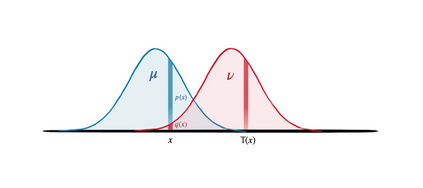
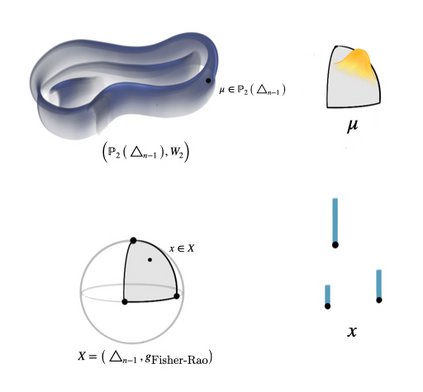
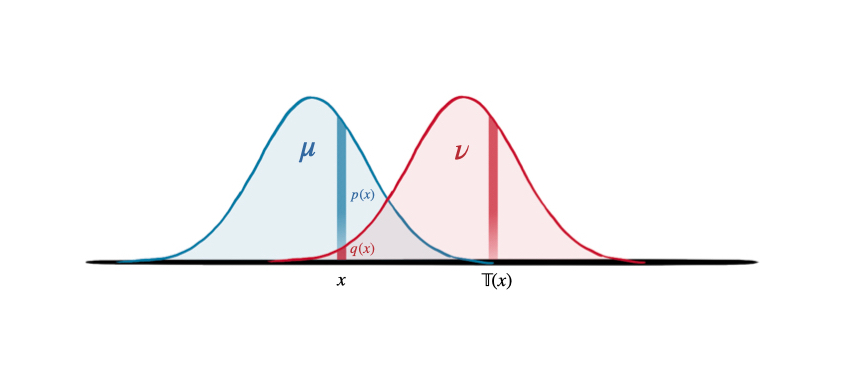
Information geometry and optimal transport are two distinct geometric frameworks for modeling families of probability measures. During the recent years, there has been a surge of research endeavors that cut across these two areas and explore their links and interactions. This paper is intended to provide an (incomplete) survey of these works, including entropy-regularized transport, divergence functions arising from $c$-duality, density manifolds and transport information geometry, the para-K\"ahler and K\"ahler geometries underlying optimal transport and the regularity theory for its solutions. Some outstanding questions that would be of interest to audience of both these two disciplines are posed. Our piece also serves as an introduction to the Special Issue on Optimal Transport of the journal Information Geometry.
翻译:信息几何和最佳运输是概率度量组建模的两个截然不同的几何框架。近年来,跨越这两个领域并探索其联系和相互作用的研究工作激增。本文件旨在提供对这些工程的(不完整的)调查,包括环球正规化运输、美元质量产生的差异功能、密度元数和运输信息几何、最佳运输基础的准K\"艾勒和K\"艾勒地理称及其解决方案的规律理论。提出了这两个学科的受众感兴趣的一些未决问题。我们的文章还作为《最佳运输期刊信息几何学》特别版的导言。