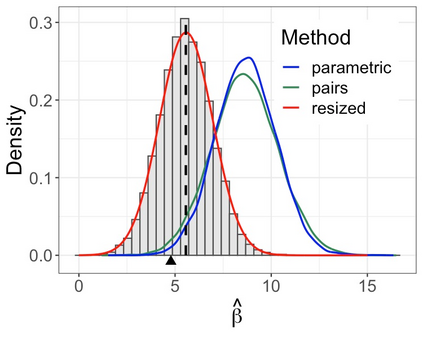
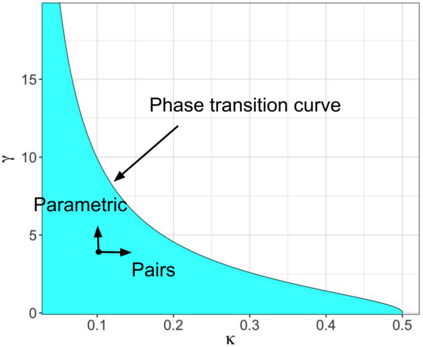
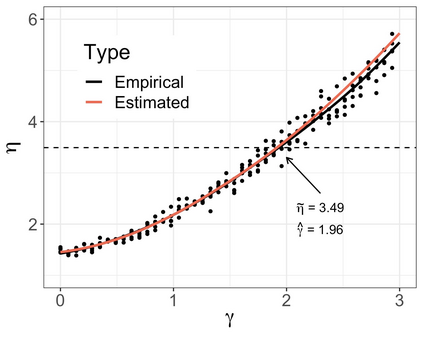
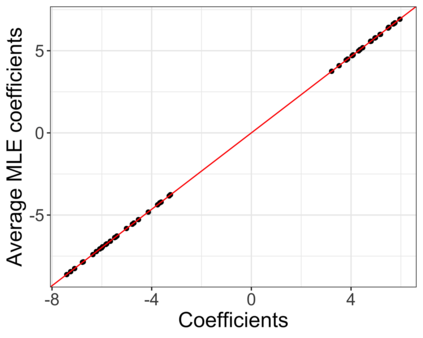
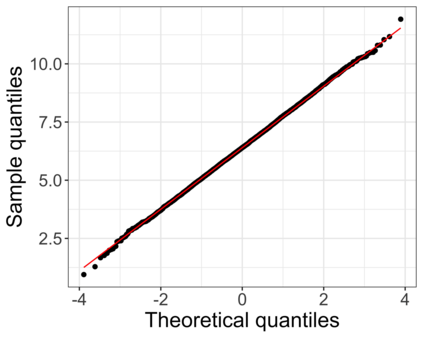
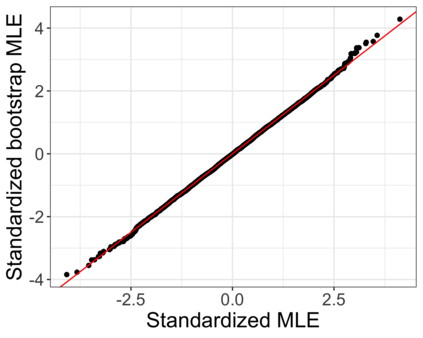
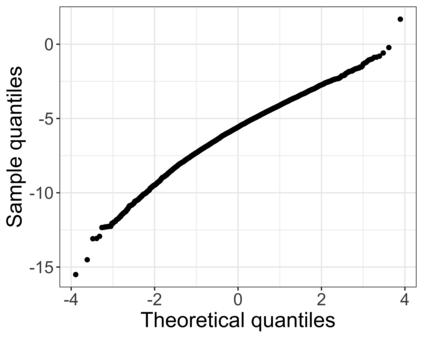
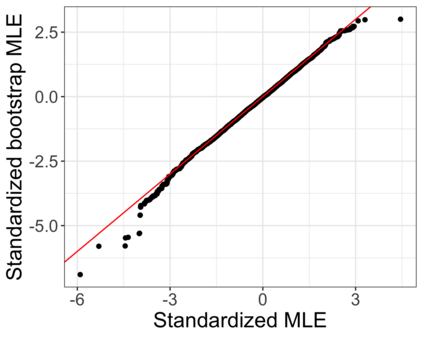
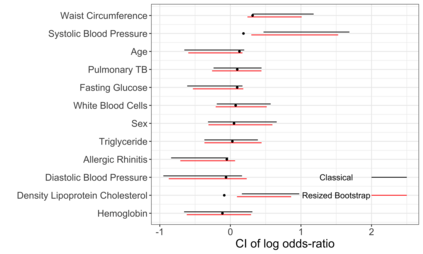
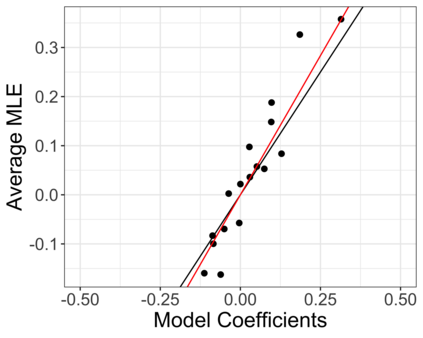
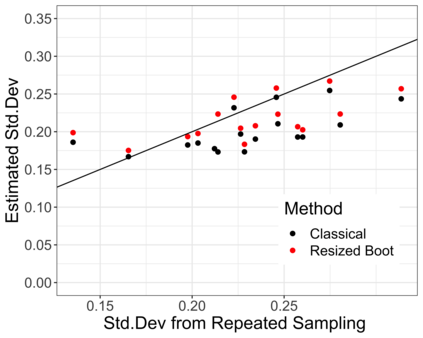
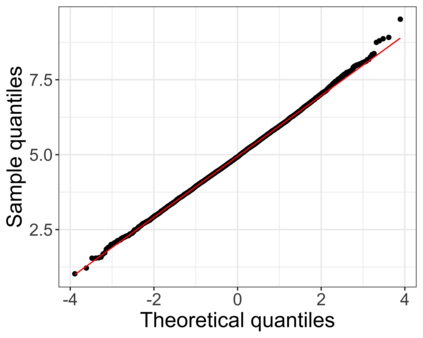
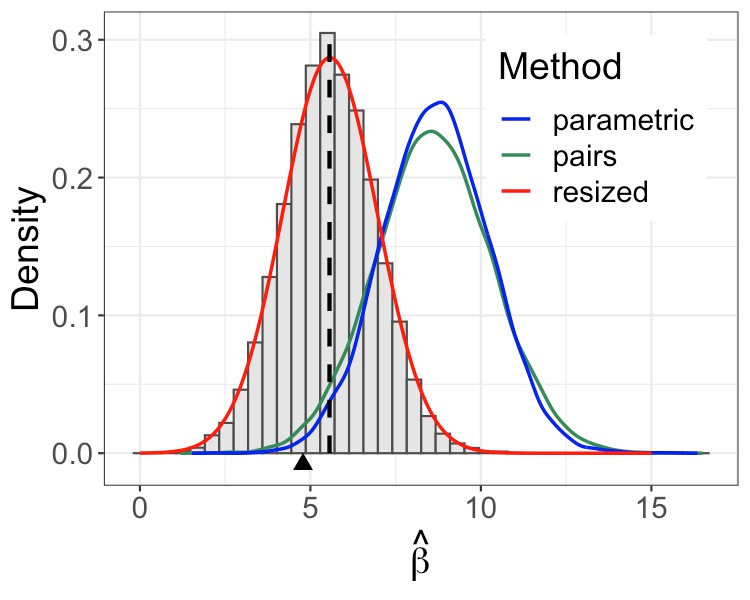
Accurate statistical inference in logistic regression models remains a critical challenge when the ratio between the number of parameters and sample size is not negligible. This is because approximations based on either classical asymptotic theory or bootstrap calculations are grossly off the mark. This paper introduces a resized bootstrap method to infer model parameters in arbitrary dimensions. As in the parametric bootstrap, we resample observations from a distribution, which depends on an estimated regression coefficient sequence. The novelty is that this estimate is actually far from the maximum likelihood estimate (MLE). This estimate is informed by recent theory studying properties of the MLE in high dimensions, and is obtained by appropriately shrinking the MLE towards the origin. We demonstrate that the resized bootstrap method yields valid confidence intervals in both simulated and real data examples. Our methods extend to other high-dimensional generalized linear models.
翻译:物流回归模型中准确的统计推论在参数数和抽样规模之间的比率不容忽略时仍是一项关键的挑战,这是因为基于古典无症状理论或靴套计算方法的近似值大大偏离了标记。本文采用了一种调整后的靴子陷阱方法来任意推算模型参数。与参数靴陷阱一样,我们从分布中重现观察,这取决于估计的回归系数序列。新颖之处在于这一估计实际上远低于最大概率估计值(MLE)。这一估计值参考了最近研究高维度MLE特性的理论,并且通过适当缩小MLE到源头而获得。我们证明,在模拟和真实数据示例中,调整后的靴子陷阱方法产生了有效的信任间隔。我们的方法扩展到了其他高维通用线性模型。