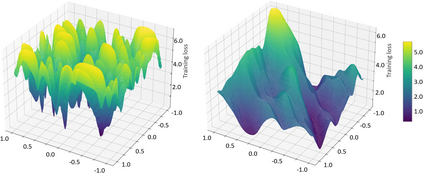
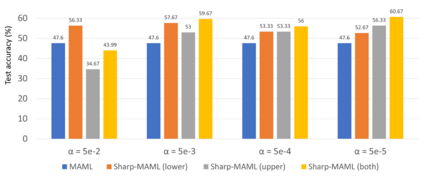
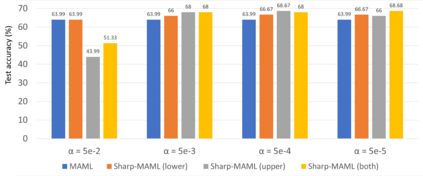
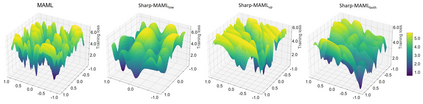
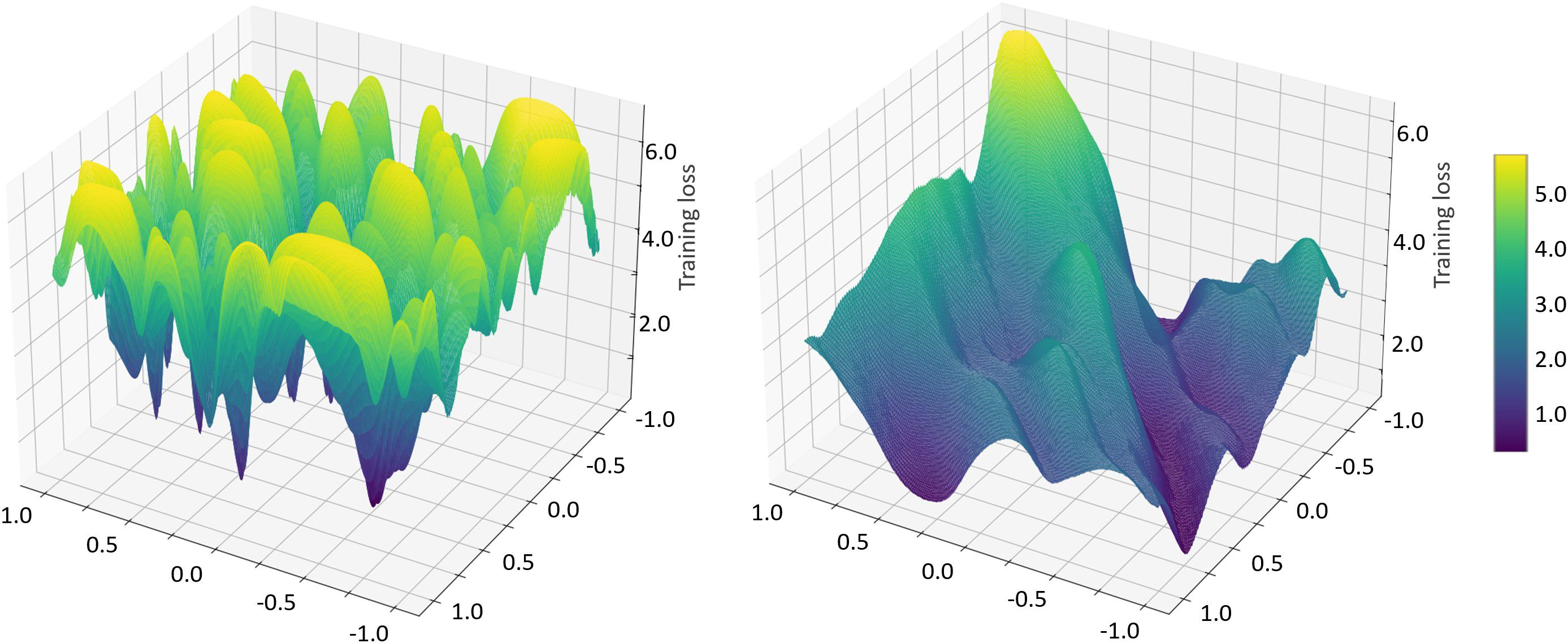
Model-agnostic meta learning (MAML) is currently one of the dominating approaches for few-shot meta-learning. Albeit its effectiveness, the optimization of MAML can be challenging due to the innate bilevel problem structure. Specifically, the loss landscape of MAML is much more complex with possibly more saddle points and local minimizers than its empirical risk minimization counterpart. To address this challenge, we leverage the recently invented sharpness-aware minimization and develop a sharpness-aware MAML approach that we term Sharp-MAML. We empirically demonstrate that Sharp-MAML and its computation-efficient variant can outperform popular existing MAML baselines (e.g., $+12\%$ accuracy on Mini-Imagenet). We complement the empirical study with the convergence rate analysis and the generalization bound of Sharp-MAML. To the best of our knowledge, this is the first empirical and theoretical study on sharpness-aware minimization in the context of bilevel learning. The code is available at https://github.com/mominabbass/Sharp-MAML.
翻译:模型-不可知元学习(MAML)目前是少数元元学习的主要方法之一。尽管其有效性是有效的,但优化MAML可能由于内在的双层问题结构而具有挑战性。具体地说,MAML的丧失面貌比其经验性风险最小化的对口单位更为复杂,可能有更多的搭载点和当地最小化因素。为了应对这一挑战,我们利用最近发明的敏锐-觉悟最小化(MAML),并发展一种我们称为Sharp-MAML的敏锐-觉悟MAML方法。我们的经验证明,Sharp-MAML及其计算效率变异体能够超过现有的MAML基准(例如,在微型-IMGnet上,美元+12+$/美元精度)。我们用趋同率分析以及将Sharp-MAML捆绑起来的通用方法补充了经验性研究。我们最了解的是,这是关于双级学习中尖化-敏化-敏化最小化的第一次经验和理论研究。我们可在https://github.com/mominabass/Sharp-Malibass/Sharp-MAML。