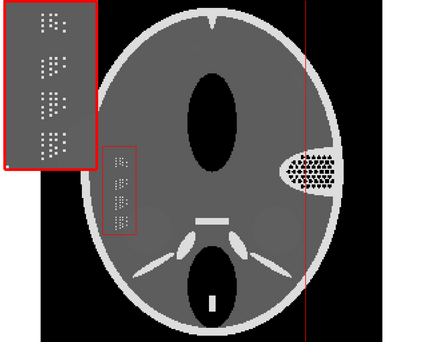
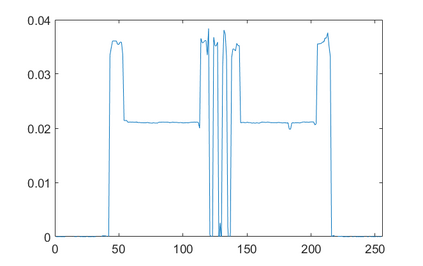
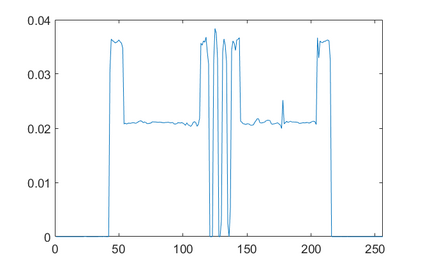
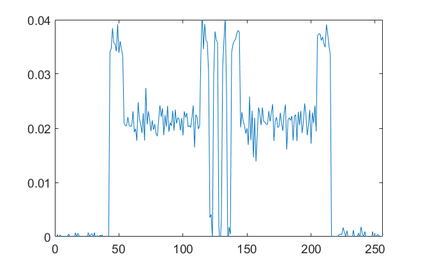
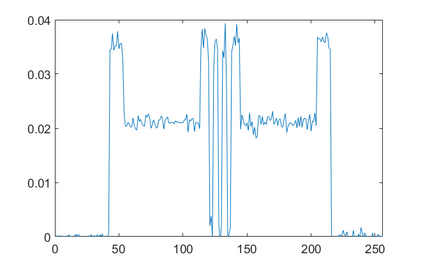
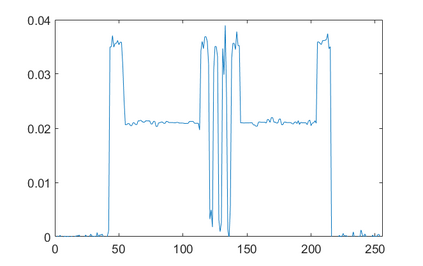
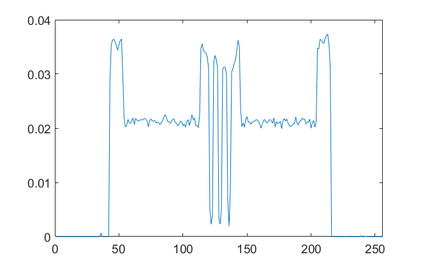
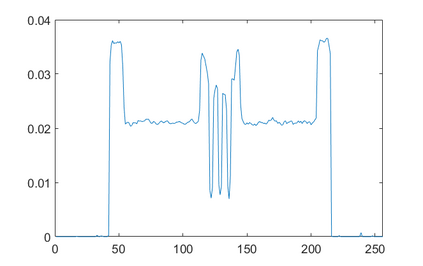
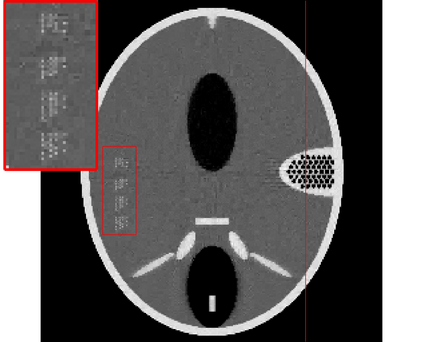
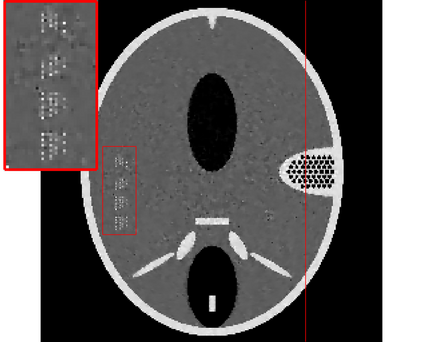
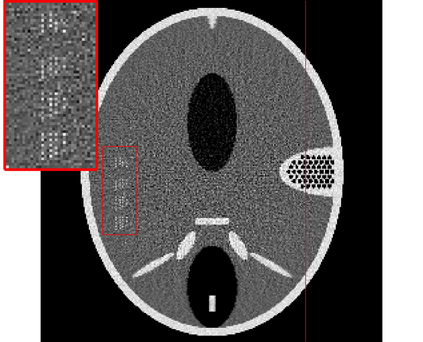
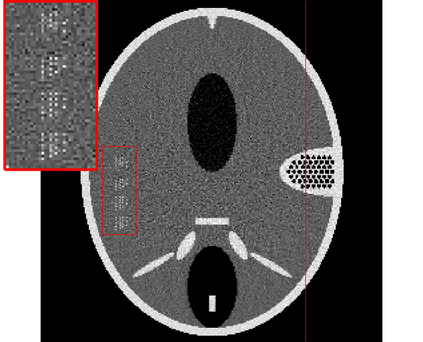
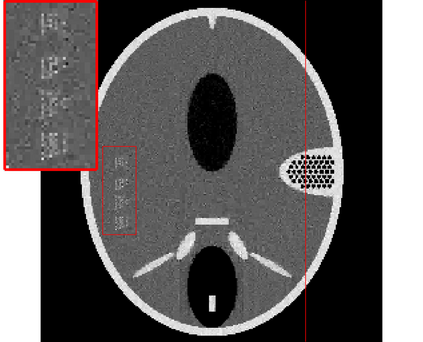
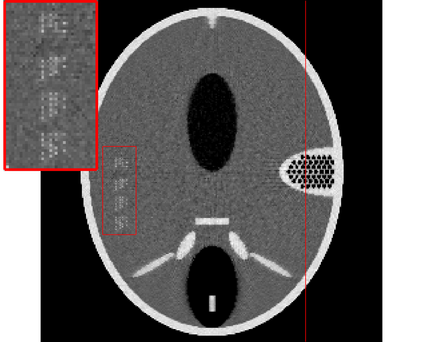
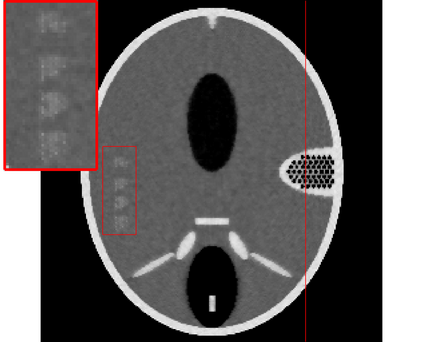
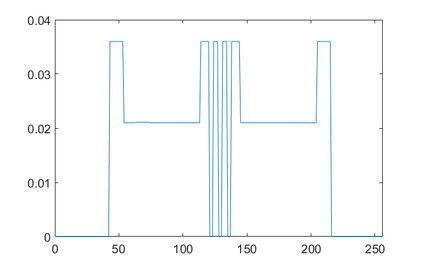
In the classic sparsity-driven problems, the fundamental L-1 penalty method has been shown to have good performance in reconstructing signals for a wide range of problems. However this performance relies on a good choice of penalty weight which is often found from empirical experiments. We propose an algorithm called the Laplacian variational automatic relevance determination (Lap-VARD) that takes this penalty weight as a parameter of a prior Laplace distribution. Optimization of this parameter using an automatic relevance determination framework results in a balance between the sparsity and accuracy of signal reconstruction. Our algorithm is implemented in a transmission tomography model with sparsity constraint in wavelet domain.
翻译:在典型的聚变驱动问题中,基本的L-1处罚方法已证明在重建广泛问题的信号方面表现良好。然而,这一绩效依赖于对刑罚重量的良好选择,而这种选择往往是从实验实验中找到的。我们提出了一种算法,称为拉普拉西亚变式自动适切性确定(Lap-VARD),该算法将这一罚款权重作为先前Laplace分布的一个参数。使用自动适切性确定框架优化这一参数,在信号重建的宽度和准确性之间取得平衡。我们的算法是在波盘域内带有宽度限制的传输断层摄影模型中实施的。