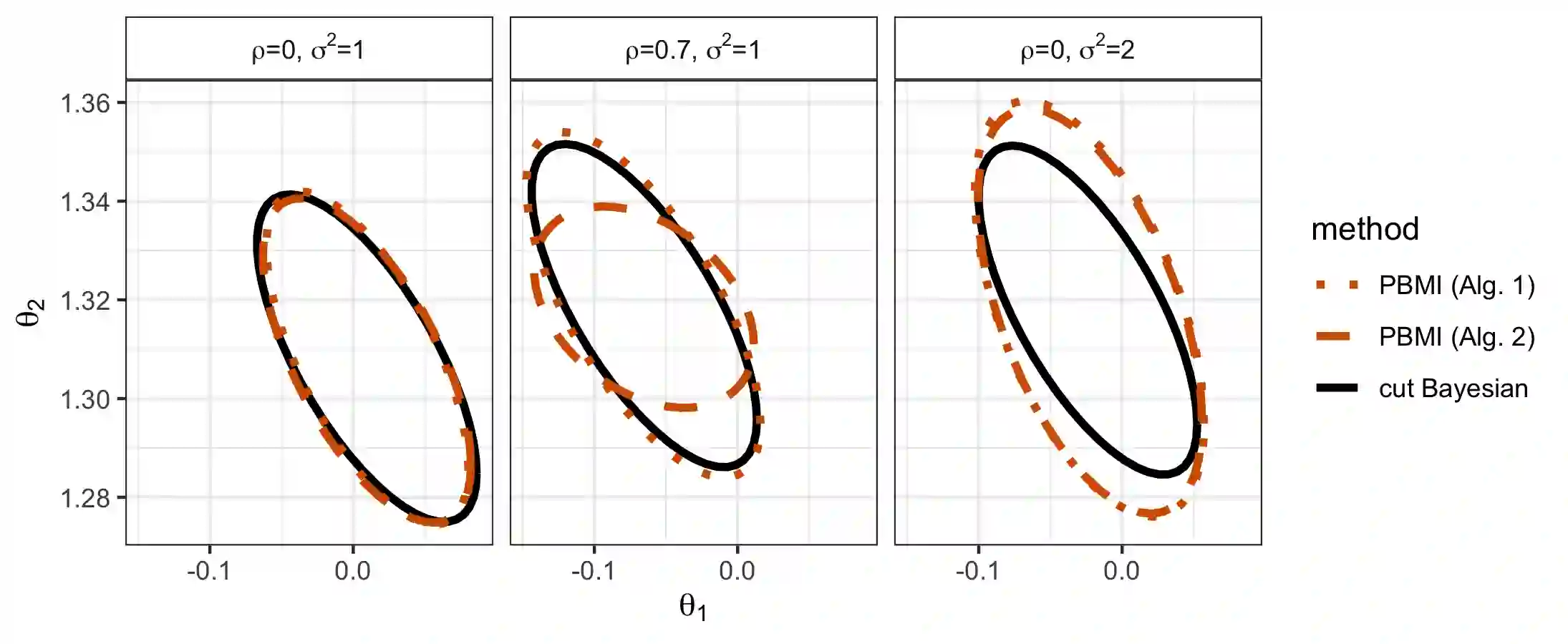
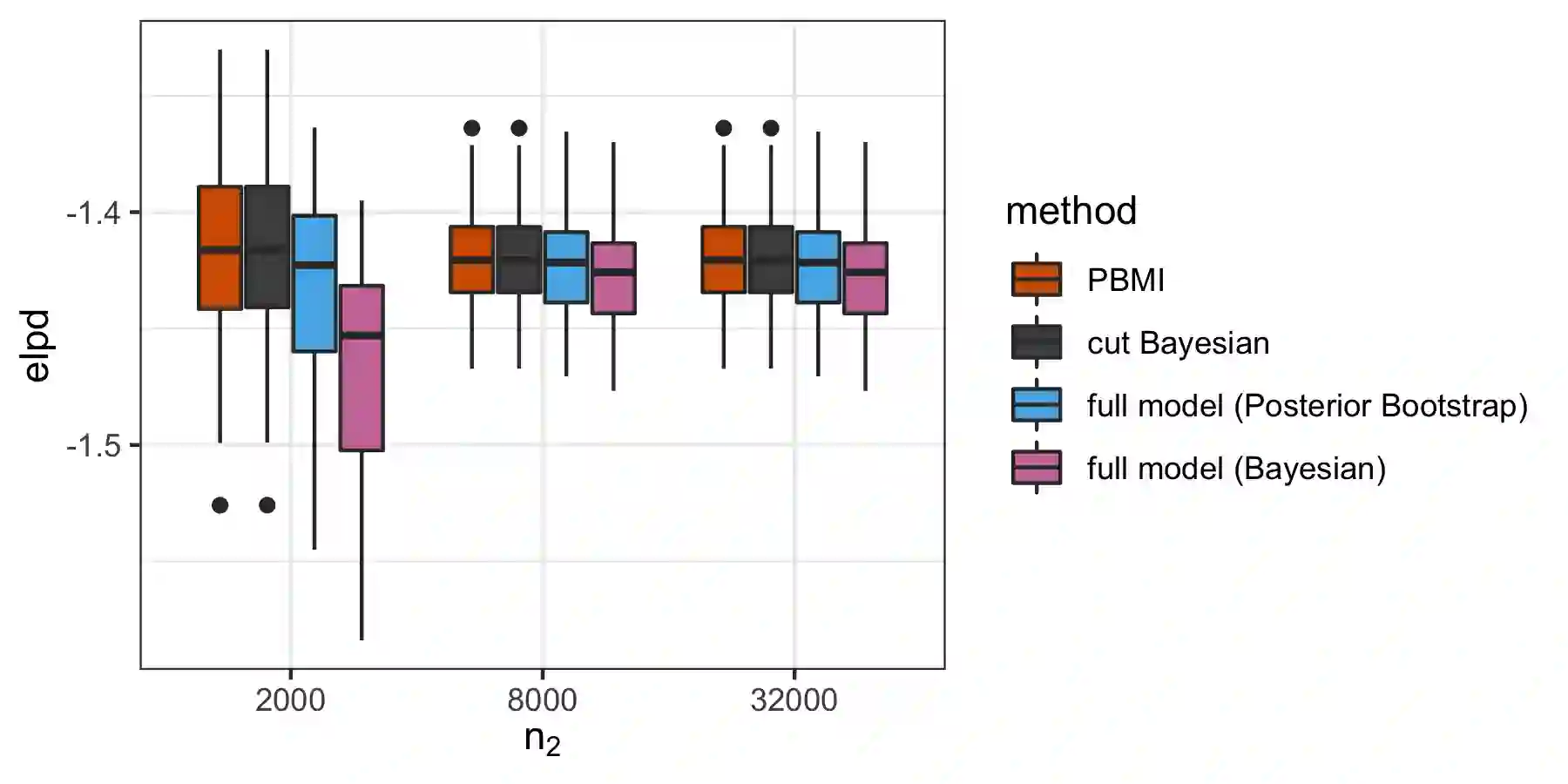
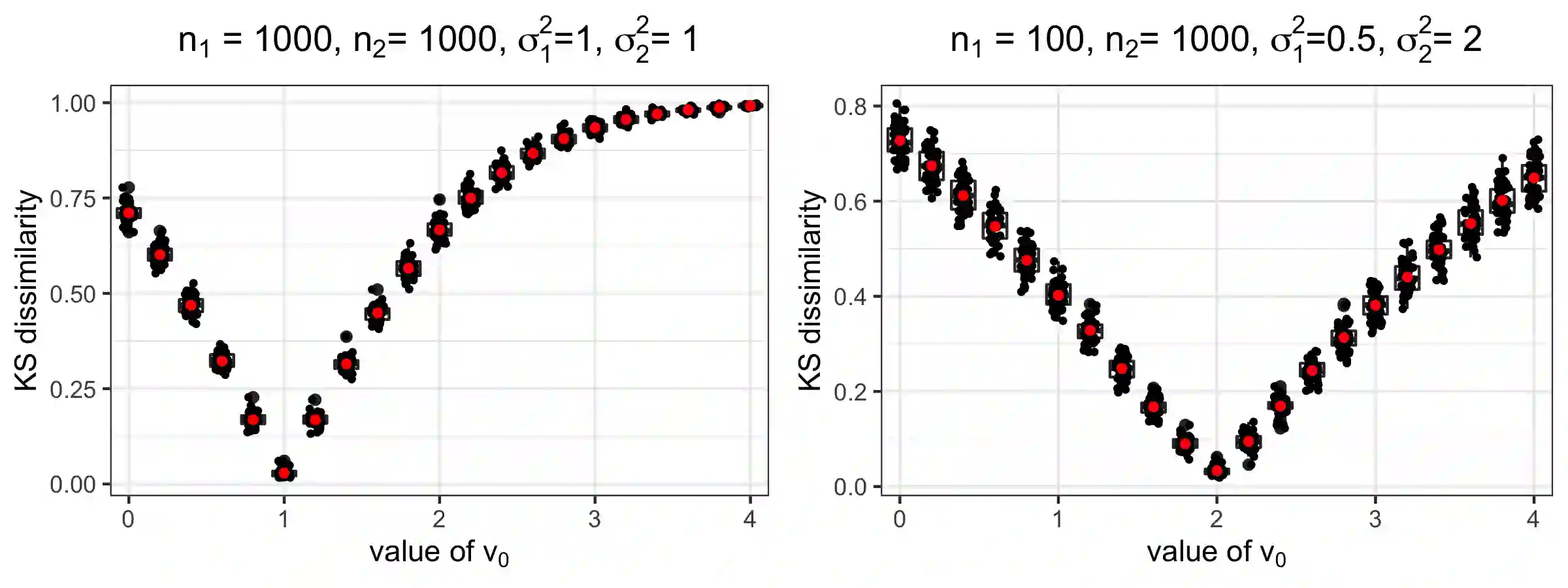
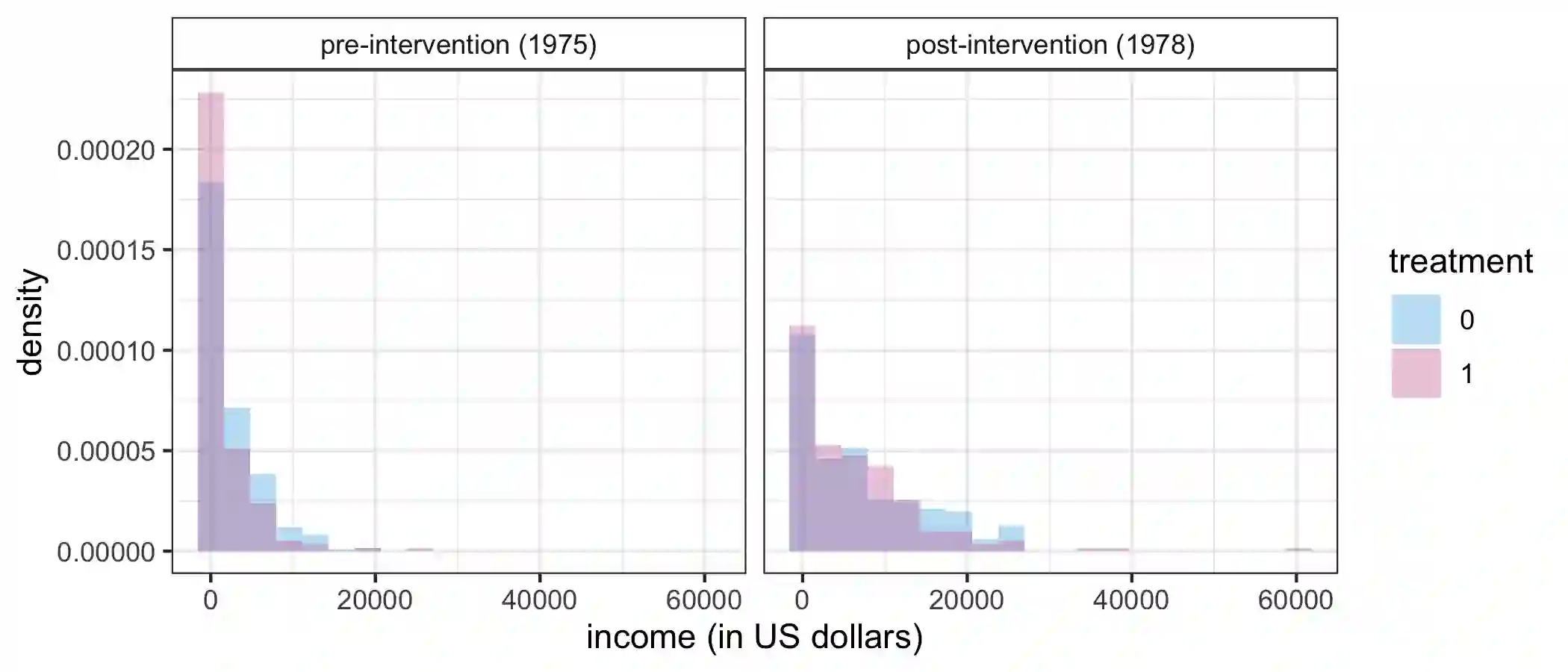
Bayesian inference provides a framework to combine an arbitrary number of model components with shared parameters, allowing joint uncertainty estimation and the use of all available data sources. However, misspecification of any part of the model might propagate to all other parts and lead to unsatisfactory results. Cut distributions have been proposed as a remedy, where the information is prevented from flowing along certain directions. We consider cut distributions from an asymptotic perspective, find the equivalent of the Laplace approximation, and notice a lack of frequentist coverage for the associate credible regions. We propose algorithms based on the Posterior Bootstrap that deliver credible regions with the nominal frequentist asymptotic coverage. The algorithms involve numerical optimization programs that can be performed fully in parallel. The results and methods are illustrated in various settings, such as causal inference with propensity scores and epidemiological studies.
翻译:贝叶斯推论提供了一个框架,将任意数量的模型组成部分与共享参数结合起来,允许共同进行不确定性估计和使用所有可用数据源。然而,模型中任何部分的分类错误可能会传播到所有其他部分,并导致不满意的结果。 提议削减分布作为一种补救措施,在信息无法沿着某些方向流动的情况下,可以这样做。 我们从无药可循的角度考虑削减分布,找到与拉帕热近似值相当的近似值,并注意缺乏对相关可靠区域的经常性覆盖。 我们提议基于Poswiter Boots陷阱的算法,这些算法可以提供具有名义常住无药覆盖度的可信区域。 算法涉及数字优化方案,可以完全平行地进行。 其结果和方法在各种环境中都得到了说明,例如与偏差分和流行病学研究的因果关系。