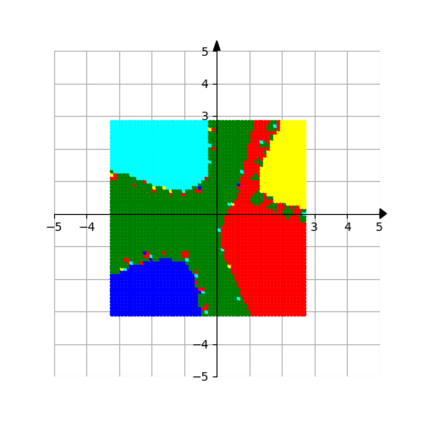
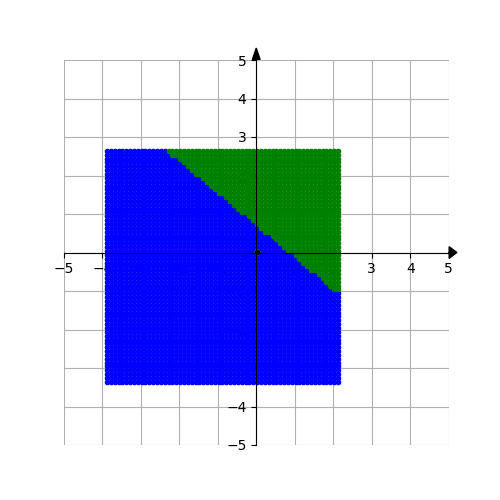
In this paper, by combining the algorithm New Q-Newton's method - developed in previous joint work of the author - with Armijo's Backtracking line search, we resolve convergence issues encountered by Newton's method (e.g. convergence to a saddle point or having attracting cycles of more than 1 point) while retaining the quick rate of convergence for Newton's method. We also develop a family of such methods, for general second order methods, some of them having the favour of quasi-Newton's methods. The developed algorithms are very easy to implement. From a Dynamical Systems' viewpoint, the new iterative method has an interesting feature: while it is deterministic, its dependence on Armijo's Backtracking line search makes its behave like a random process, and thus helps it to have good performance. On the experimental aspect, we compare the performance of our algorithms with well known variations of Newton's method on some systems of equations (both real and complex variables). We also explore some basins of attraction arising from Backtracking New Q-Newton's method, which seem to be quite regular and do not have the fractal structures as observed for the standard Newton's method. Basins of attraction for Backtracking Gradient Descent seem not be that regular.
翻译:在本文中,我们通过将新Q-Newton的算法方法(在作者先前的联合工作中开发的新Q-Newton的算法-与Armijo的回溯跟踪线搜索相结合,解决了牛顿方法遇到的趋同问题(例如,趋同到一个马鞍点或吸引周期超过1个点),同时保留牛顿方法的快速趋同率。我们还开发了这种方法的组合,用于一般的第二顺序方法,其中一些方法优于准纽顿方法。发达的算法非常容易实施。从动态系统的观点来看,新的迭代方法有一个有趣的特征:虽然它具有确定性,但依赖Armijo的回溯跟踪线搜索使它的行为像一个随机的过程,从而帮助它取得良好的业绩。在实验方面,我们比较了我们算法的性能与人们熟知的牛顿方法在某些方程系统(包括真实和复杂的变量)上的变异性。我们还探索了从回溯跟踪新Q-Newton系统中产生的吸引力基础,我们还探索了一种吸引基础,而后回溯看它似乎不是常规的后行法系,而后行法则则似乎是典型。