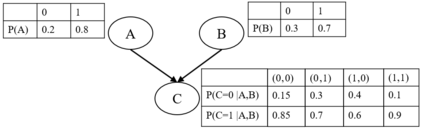
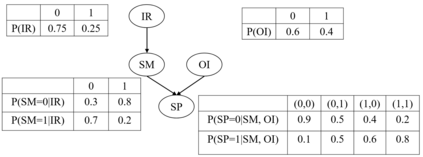
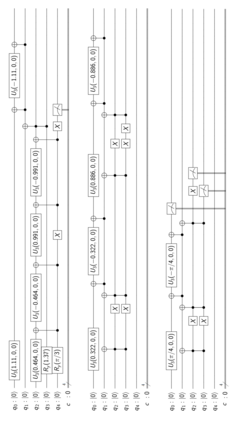
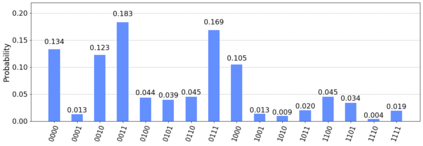
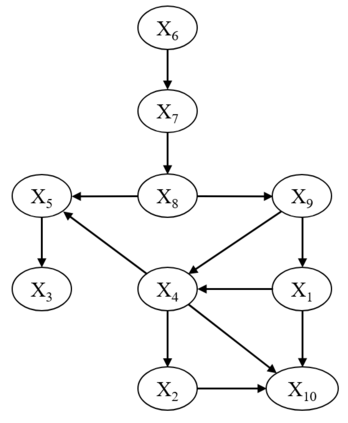
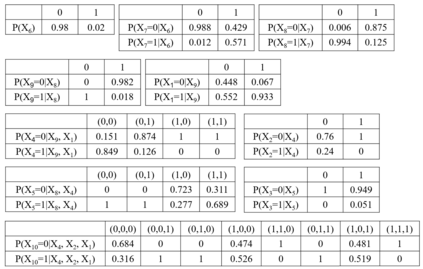
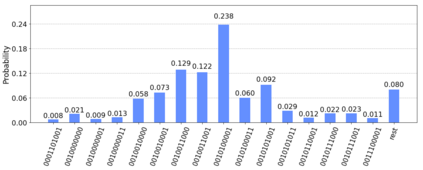
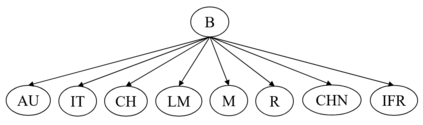
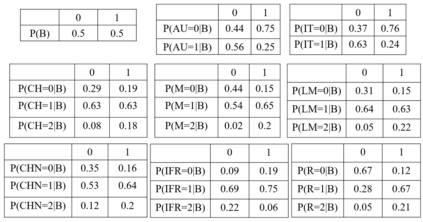
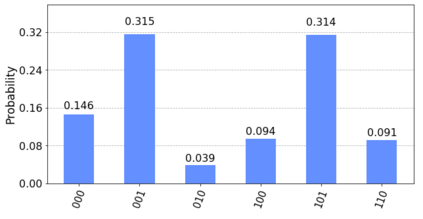
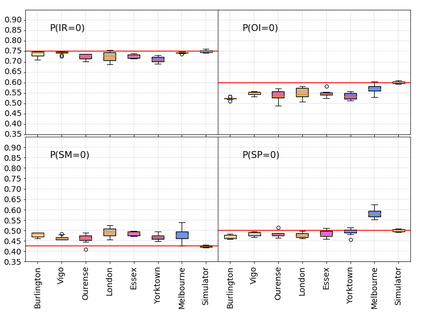
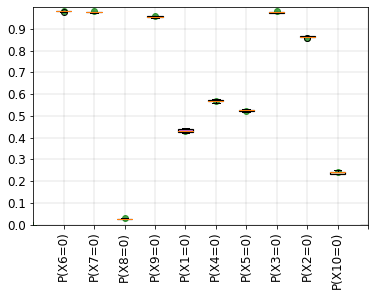
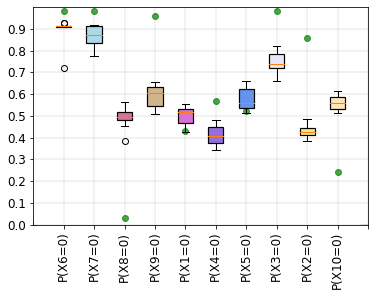
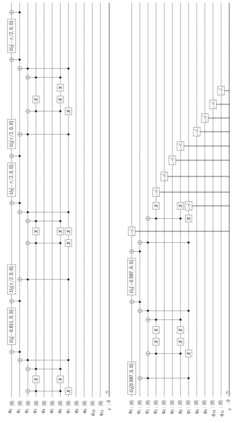
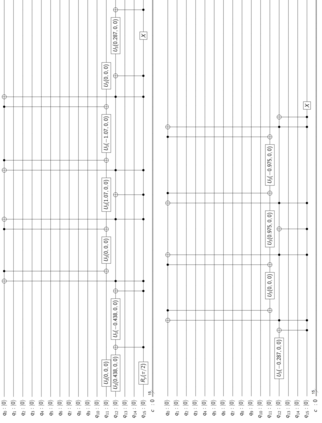
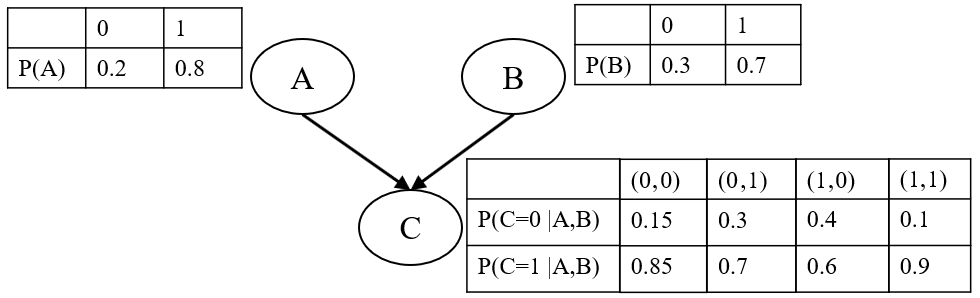
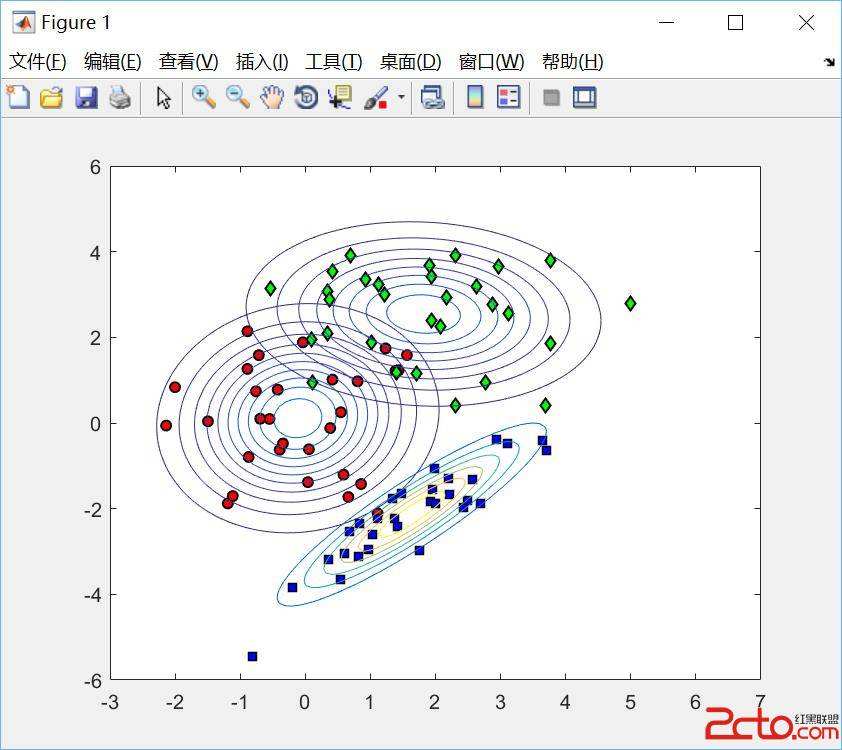
Probabilistic graphical models such as Bayesian networks are widely used to model stochastic systems to perform various types of analysis such as probabilistic prediction, risk analysis, and system health monitoring, which can become computationally expensive in large-scale systems. While demonstrations of true quantum supremacy remain rare, quantum computing applications managing to exploit the advantages of amplitude amplification have shown significant computational benefits when compared against their classical counterparts. We develop a systematic method for designing a quantum circuit to represent a generic discrete Bayesian network with nodes that may have two or more states, where nodes with more than two states are mapped to multiple qubits. The marginal probabilities associated with root nodes (nodes without any parent nodes) are represented using rotation gates, and the conditional probability tables associated with non-root nodes are represented using controlled rotation gates. The controlled rotation gates with more than one control qubit are represented using ancilla qubits. The proposed approach is demonstrated for three examples: a 4-node oil company stock prediction, a 10-node network for liquidity risk assessment, and a 9-node naive Bayes classifier for bankruptcy prediction. The circuits were designed and simulated using Qiskit, a quantum computing platform that enables simulations and also has the capability to run on real quantum hardware. The results were validated against those obtained from classical Bayesian network implementations.
翻译:Bayesian网络等概率图形模型被广泛用于模拟随机系统,以进行各种类型的分析,如概率预测、风险分析和系统健康监测,这种分析在大规模系统中可能变得成本高昂。虽然真正的量子至上演示仍然很少,但量子计算应用程序在利用振幅振幅放大的优势方面表现出巨大的计算效益,与古老的对口相比,这显示出了巨大的计算效益。我们开发了一个系统的方法来设计量子电路,以代表一个通用的离散的Bayesian网络,其节点可能有两个或两个以上的国家,其中两个以上的国家的节点被映射到多个qubit。根节点(没有任何母节点的节点的节点)相关的边际概率在使用旋转门,而与非根节点相关的有条件概率表则使用受控的旋转门。一个以上控制方位的受控的旋转门使用ancilla qubits。拟议的方法有三个例子:一个4node石油公司库存预测,一个用于流动性风险评估的10node网络,以及一个9nobes IMBaysalal comal comalal compeal 也使这些模型能够进行模拟运行。