Pattern recovery and signal denoising by SLOPE when the design matrix is orthogonal

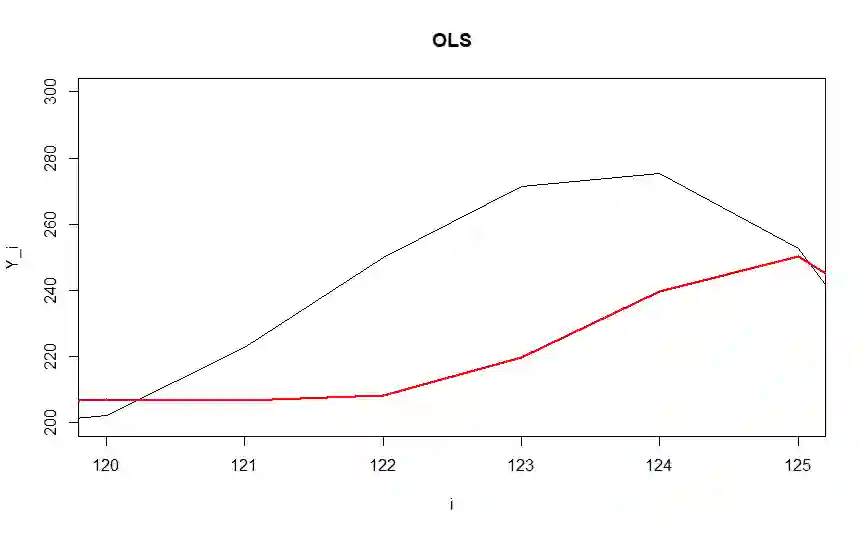
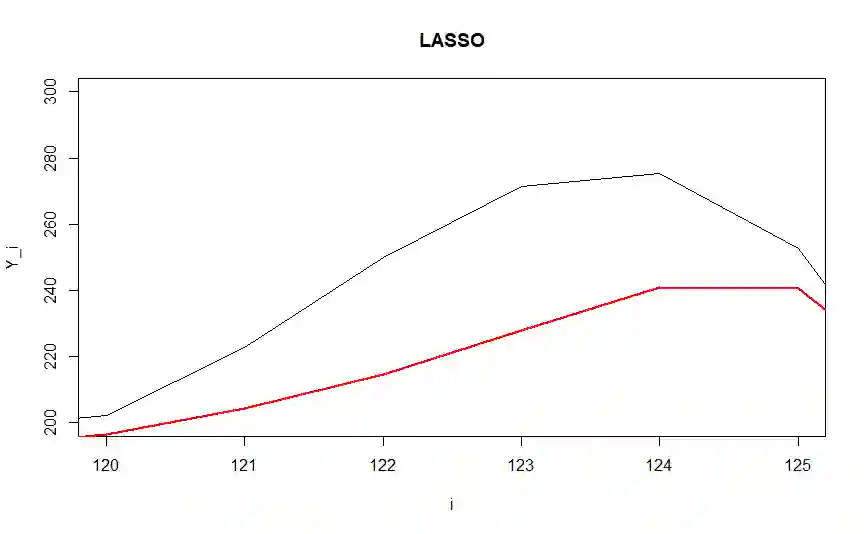
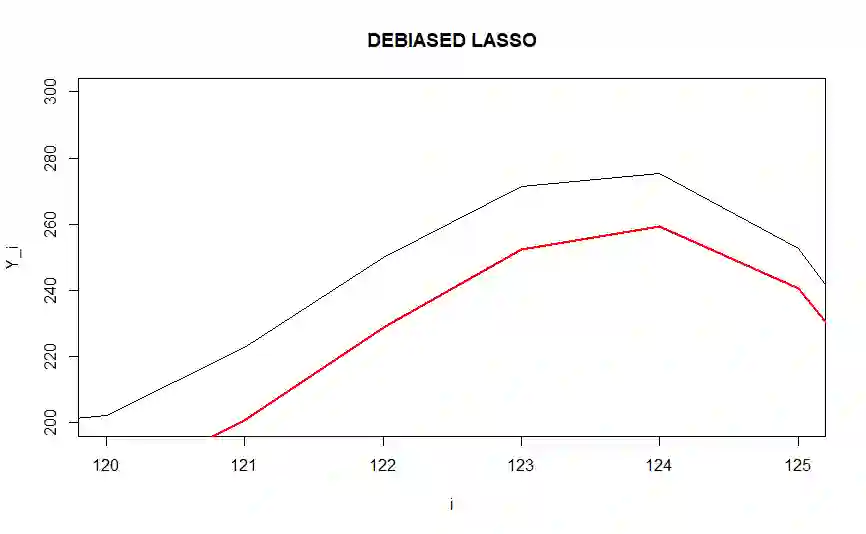
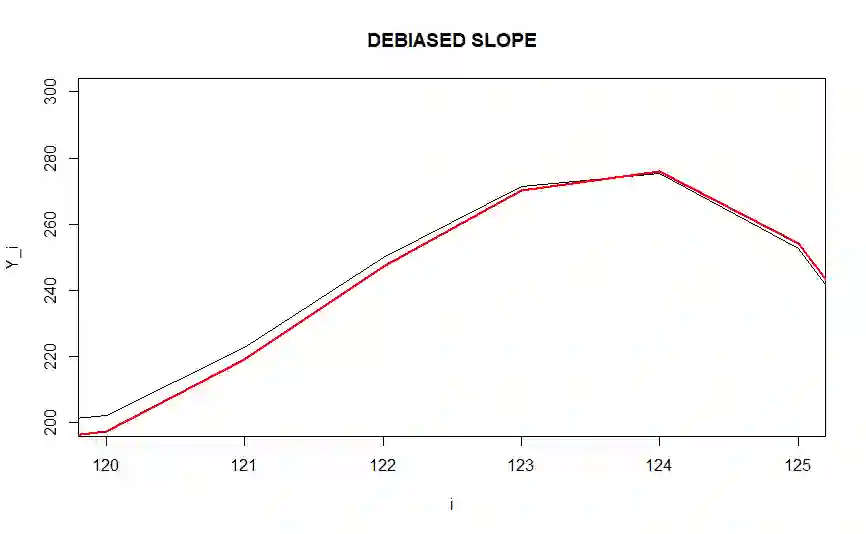
Sorted $\ell_1$ Penalized Estimator (SLOPE) is a relatively new convex regularization method for fitting high-dimensional regression models. SLOPE allows to reduce the model dimension by shrinking some estimates of the regression coefficients completely to zero or by equating the absolute values of some nonzero estimates of these coefficients. This allows to identify situations where some of~true regression coefficients are equal. In this article we will introduce the SLOPE pattern, i.e., the set of relations between the true regression coefficients, which can be identified by SLOPE. We will also present new results on the strong consistency of SLOPE estimators and on~the~strong consistency of pattern recovery by~SLOPE when the design matrix is orthogonal and illustrate advantages of~the~SLOPE clustering in the context of high frequency signal denoising.