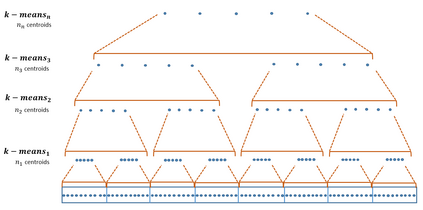
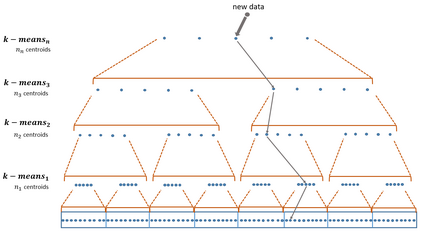
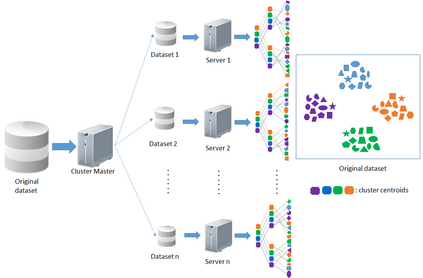
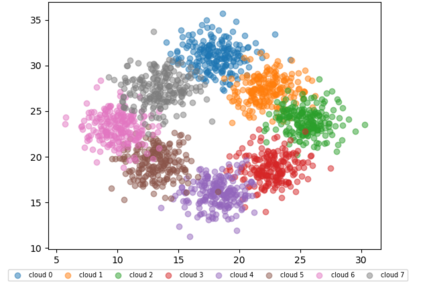
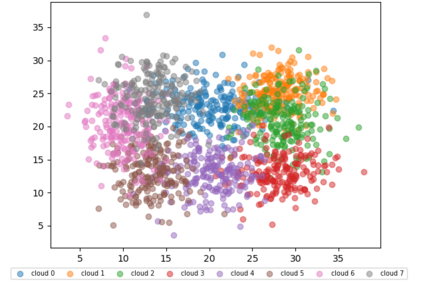
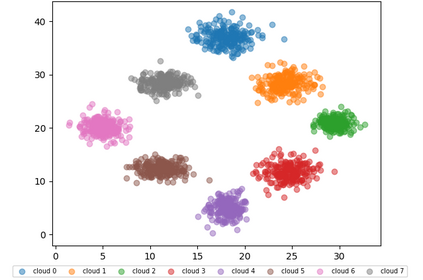
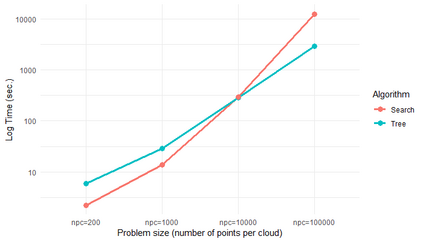
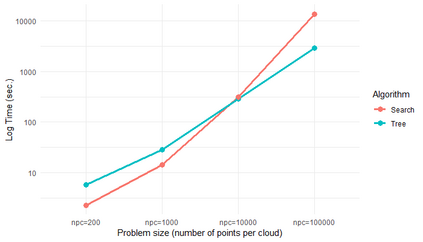
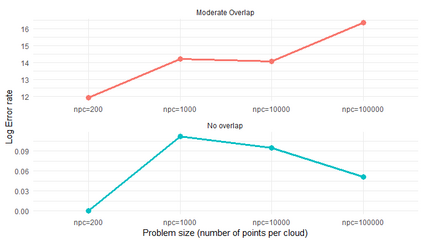
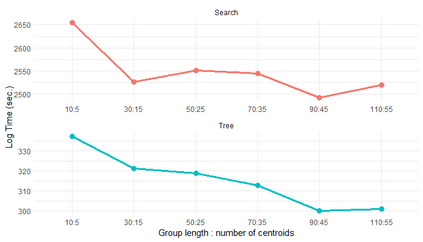
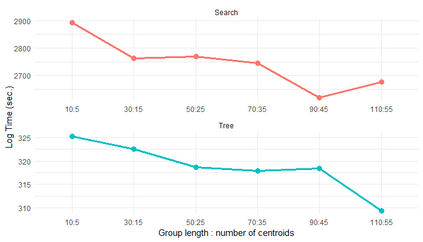
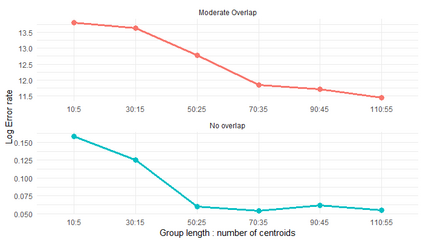
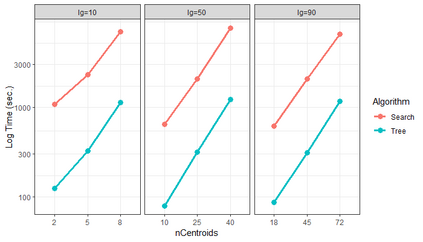
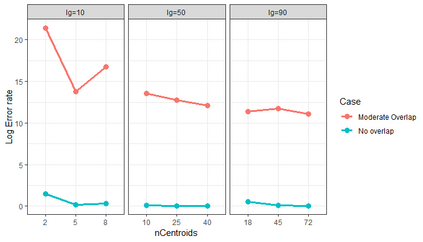
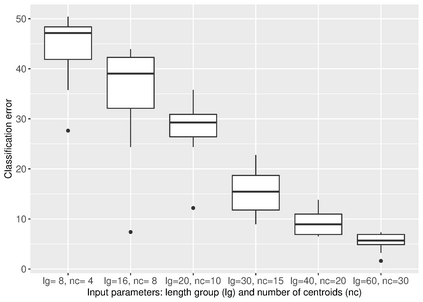
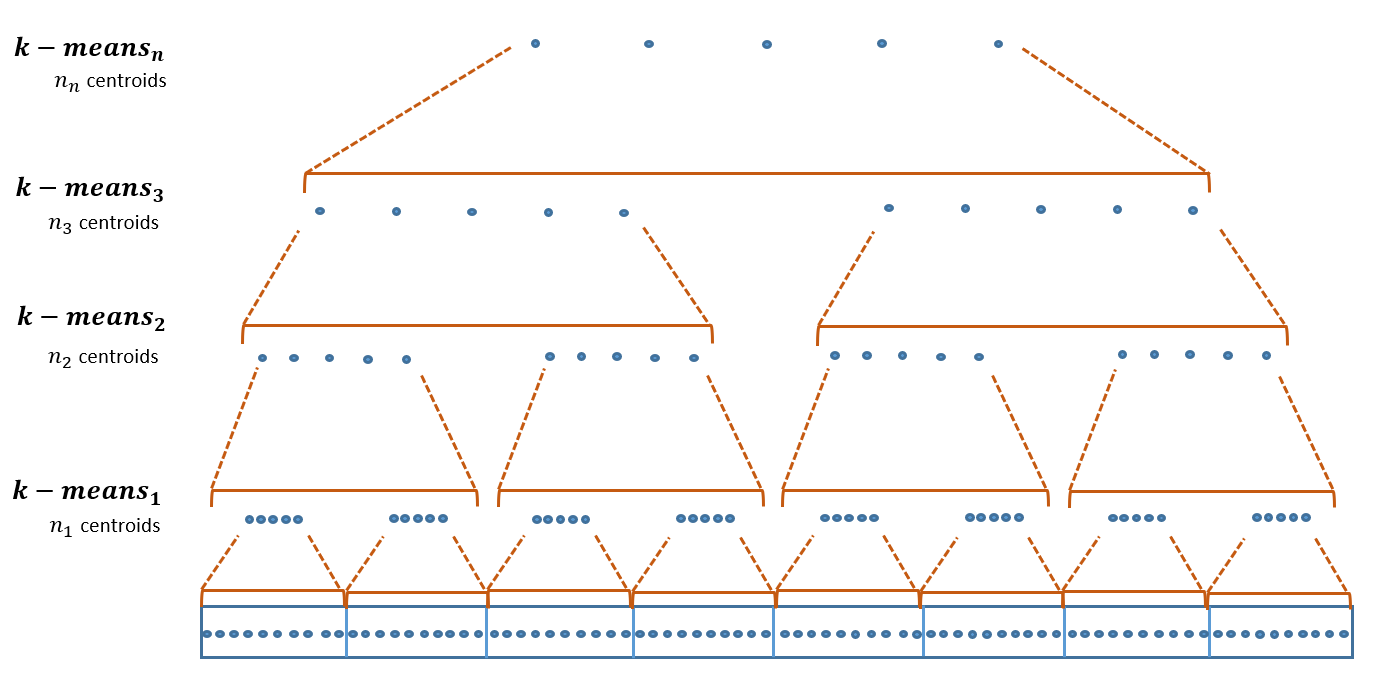
Similarity search based on a distance function in metric spaces is a fundamental problem for many applications. Queries for similar objects lead to the well-known machine learning task of nearest-neighbours identification. Many data indexing strategies, collectively known as Metric Access Methods (MAM), have been proposed to speed up queries for similar elements in this context. Moreover, since exact approaches to solve similarity queries can be complex and time-consuming, alternative options have appeared to reduce query execution time, such as returning approximate results or resorting to distributed computing platforms. In this paper, we introduce MASK (Multilevel Approximate Similarity search with $k$-means), an unconventional application of the $k$-means algorithm as the foundation of a multilevel index structure for approximate similarity search, suitable for metric spaces. We show that inherent properties of $k$-means, like representing high-density data areas with fewer prototypes, can be leveraged for this purpose. An implementation of this new indexing method is evaluated, using a synthetic dataset and a real-world dataset in a high-dimensional and high-sparsity space. Results are promising and underpin the applicability of this novel indexing method in multiple domains.
翻译:在测量空间的距离函数基础上进行相似性搜索是许多应用的根本问题。 类似对象的查询导致众所周知的近邻居民身份识别的机器学习任务。 许多数据索引战略(统称为Metric Access 方法(MAM))已经建议在此背景下加快对类似元素的查询。 此外,由于解决相似性查询的精确方法可能复杂而费时, 替代选项似乎减少了查询执行时间, 如返回近似结果或使用分布式计算平台。 在本文中, 我们引入了MASK( Multial Aprearal Aprearity搜索以美元表示近似相似性), 将美元手段算法作为近似相似性搜索的多级指数结构的基础, 适用于度空间。 我们显示, 美元手段的固有特性, 如代表高密度数据区域, 原型较少, 可用于此目的。 使用合成数据集和在高度和高度空间基础域中真实世界数据集来评估这一新索引方法的采用情况。