Selective Machine Learning of the Average Treatment Effect with an Invalid Instrumental Variable

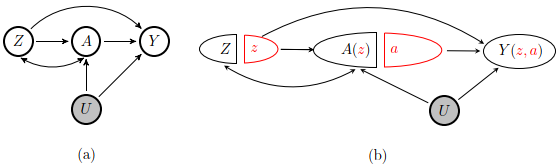
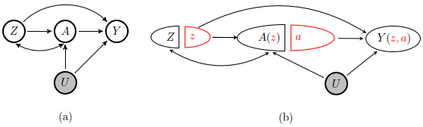
Instrumental variable methods have been widely used to identify causal effects in the presence of unmeasured confounding. A key identification condition known as the exclusion restriction states that the instrument cannot have a direct effect on the outcome which is not mediated by the exposure in view. In the health and social sciences, such an assumption is often not credible. To address this concern, we consider identification conditions of the population average treatment effect with an invalid instrumental variable which does not satisfy the exclusion restriction, and derive the efficient influence function targeting the identifying functional under a nonparametric observed data model. We propose a novel multiply robust locally efficient estimator of the average treatment effect that is consistent in the union of multiple parametric nuisance models, as well as a multiply debiased machine learning estimator for which the nuisance parameters are estimated using generic machine learning methods, that effectively exploit various forms of linear or nonlinear structured sparsity in the nuisance parameter space. When one cannot be confident that any of these machine learners is consistent at sufficiently fast rates to ensure $\surd{n}$-consistency for the average treatment effect, we introduce a new criteria for selective machine learning which leverages the multiple robustness property in order to ensure small bias. The proposed methods are illustrated through extensive simulations and a data analysis evaluating the causal effect of 401(k) participation on savings.