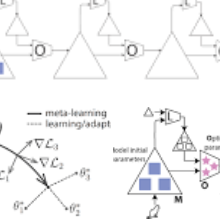
Meta-learning, or "learning to learn", refers to techniques that infer an inductive bias from data corresponding to multiple related tasks with the goal of improving the sample efficiency for new, previously unobserved, tasks. A key performance measure for meta-learning is the meta-generalization gap, that is, the difference between the average loss measured on the meta-training data and on a new, randomly selected task. This paper presents novel information-theoretic upper bounds on the meta-generalization gap. Two broad classes of meta-learning algorithms are considered that uses either separate within-task training and test sets, like MAML, or joint within-task training and test sets, like Reptile. Extending the existing work for conventional learning, an upper bound on the meta-generalization gap is derived for the former class that depends on the mutual information (MI) between the output of the meta-learning algorithm and its input meta-training data. For the latter, the derived bound includes an additional MI between the output of the per-task learning procedure and corresponding data set to capture within-task uncertainty. Tighter bounds are then developed, under given technical conditions, for the two classes via novel Individual Task MI (ITMI) bounds. Applications of the derived bounds are finally discussed, including a broad class of noisy iterative algorithms for meta-learning.
翻译:元学习或“学习”是指从与多项相关任务对应的数据中推断出一种感应偏差的技术,目的是提高新任务、以前未观察到的任务的抽样效率。元学习的一个关键业绩计量是元普及差距,即从元培训数据中测得的平均损失与新、随机选择的任务之间的差别。本文介绍了元普及差距的新信息-理论上限。两种广泛的元学习算法被认为使用单独的任务内培训和测试组,如MAML,或联合的任务内培训和测试组,如Reptile。扩大现有常规学习工作,从前一类中得出对元化差距的上限,取决于元学习算法产出与其输入的元培训数据之间的相互信息(MI)。对于后一类,衍生的链接包括在一次任务内学习程序的产出和用于捕获任务内不确定性的相应数据组(如MAML,或联合的任务内培训和测试组),如Reptile。扩展现有常规学习工作,后一个对元化差距的上限是前一类的上限,在技术-学习算法产出和输入的双级中,在后两个阶段讨论后,在技术级中,在后期学习的跨级中进行。