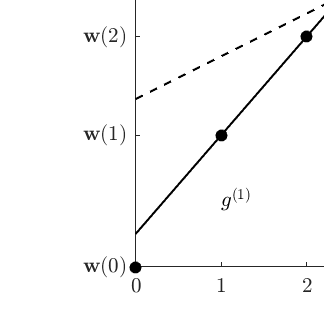
In recent years, hypergraph generalizations of many graph cut problems have been introduced and analyzed as a way to better explore and understand complex systems and datasets characterized by multiway relationships. Recent work has made use of a generalized hypergraph cut function which for a hypergraph $\mathcal{H} = (V,E)$ can be defined by associating each hyperedge $e \in E$ with a splitting function ${\bf w}_e$, which assigns a penalty to each way of separating the nodes of $e$. When each ${\bf w}_e$ is a submodular cardinality-based splitting function, meaning that ${\bf w}_e(S) = g(|S|)$ for some concave function $g$, previous work has shown that a generalized hypergraph cut problem can be reduced to a directed graph cut problem on an augmented node set. However, existing reduction procedures often result in a dense graph, even when the hypergraph is sparse, which leads to slow runtimes for algorithms that run on the reduced graph. We introduce a new framework of sparsifying hypergraph-to-graph reductions, where a hypergraph cut defined by submodular cardinality-based splitting functions is $(1+\varepsilon)$-approximated by a cut on a directed graph. Our techniques are based on approximating concave functions using piecewise linear curves. For $\varepsilon > 0$ we need at most $O(\varepsilon^{-1}|e| \log |e|)$ edges to reduce any hyperedge $e$, which leads to faster runtimes for approximating generalized hypergraph $s$-$t$ cut problems. For the machine learning heuristic of a clique splitting function, our approach requires only $O(|e| \varepsilon^{-1/2} \log \log \frac{1}{\varepsilon})$ edges. This sparsification leads to faster approximate min $s$-$t$ graph cut algorithms for certain classes of co-occurrence graphs. Finally, we apply our sparsification techniques to develop approximation algorithms for minimizing sums of cardinality-based submodular functions.
翻译:近些年来,人们引入并分析过许多图形断层问题的超常化,以此更好地探索和理解以多路关系为特征的复杂系统和数据集。最近的工作利用了通用的超常裁量功能,对于某个超光速 $\ mathcal{H} = (V,E) = (V,E),可以通过将每个高端 $\ 以 E$ 与一个分解函数 $_bf w ⁇ 美元挂钩来定义。但是,现有的降级程序往往会导致一个密度的图形,即使高平流需要一个以美元为基的美元基离层断层分解功能。我们引入了一个以美元为基的基离层平流功能框架,通过一个以美元为基的离层平流技术来将一个以美元为基的平流化。