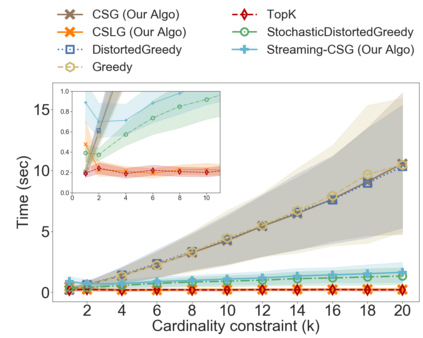
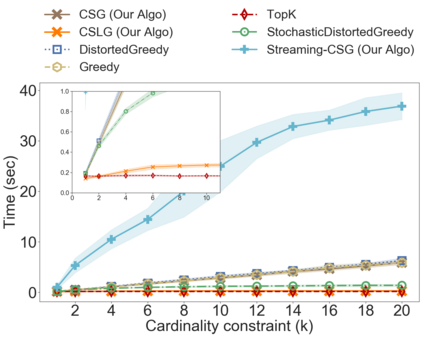
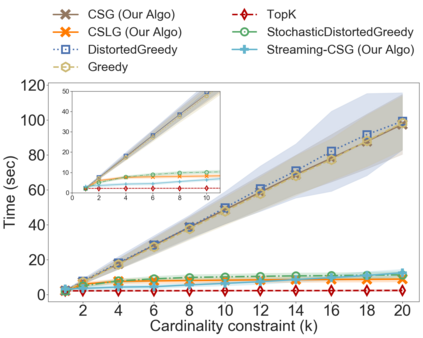
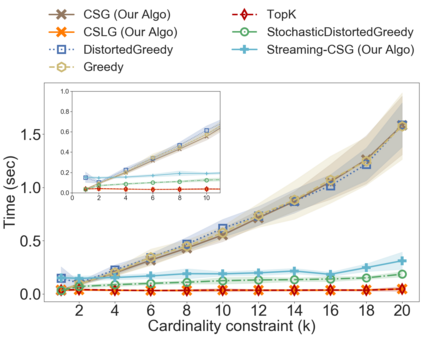
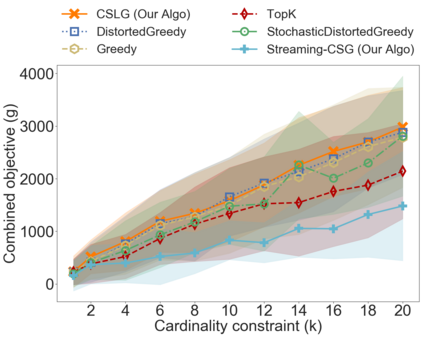
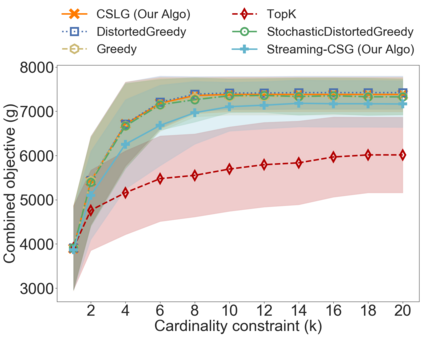
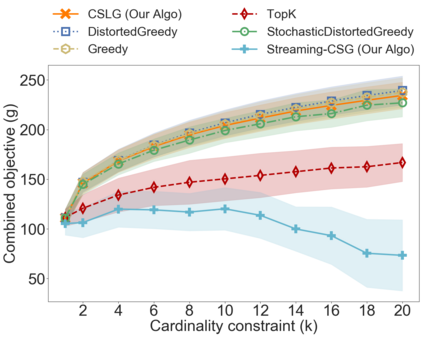
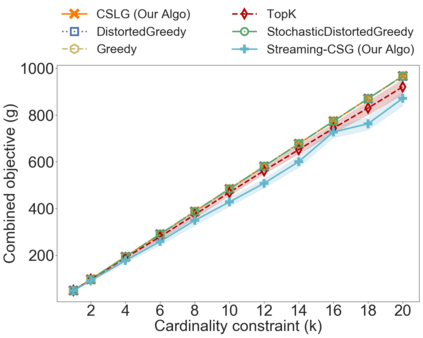
In the classical selection problem, the input consists of a collection of elements and the goal is to pick a subset of elements from the collection such that some objective function $f$ is maximized. This problem has been studied extensively in the data-mining community and it has multiple applications including influence maximization in social networks, team formation and recommender systems. A particularly popular formulation that captures the needs of many such applications is one where the objective function $f$ is a monotone and non-negative submodular function. In these cases, the corresponding computational problem can be solved using a simple greedy $(1-\frac{1}{e})$-approximation algorithm. In this paper, we consider a generalization of the above formulation where the goal is to optimize a function that maximizes the submodular function $f$ minus a linear cost function $c$. This formulation appears as a more natural one, particularly when one needs to strike a balance between the value of the objective function and the cost being paid in order to pick the selected elements. We address variants of this problem both in an offline setting, where the collection is known a priori, as well as in online settings, where the elements of the collection arrive in an online fashion. We demonstrate that by using simple variants of the standard greedy algorithm (used for submodular optimization) we can design algorithms that have provable approximation guarantees, are extremely efficient and work very well in practice.
翻译:在古典选择问题中,输入包括一个元素的集合,目标是从收集中挑选一组元素,使某些客观功能达到最大化。这个问题已经在数据采集界进行了广泛研究,并具有多种应用,包括在社交网络、团队组建和建议系统的影响最大化。一种特别流行的表达方式,它反映了许多此类应用程序的需要,一种特别流行的表达方式,其目标功能是单调和非负分调的子模块功能。在这些情况下,相应的计算问题可以通过简单的贪婪$(1-\frac{{{1 ⁇ e})美元($-frac{{{{{{{{_e})来解决。在本文中,我们考虑上述表述方式的概括化,目标是优化子模块功能的最大化,美元减去线性成本函数(c$)。这一表述方式显得更自然,特别是当人们需要平衡目标功能的价值和为选择选定要素而支付的费用时。我们在离线的设置中处理该问题的变式,即以离线方式处理问题,即我们所了解的精细的精细的排序方法,在网上的排序中,我们以最精细的排序方式收集,然后以最精细的排序方式展示了标准化的排序,在网上的排序中,我们以最精细的排序中可以展示的排序中,在网上的排序中可以展示的排序中,我们所知道的排序,以展示的排序方式展示的排序。