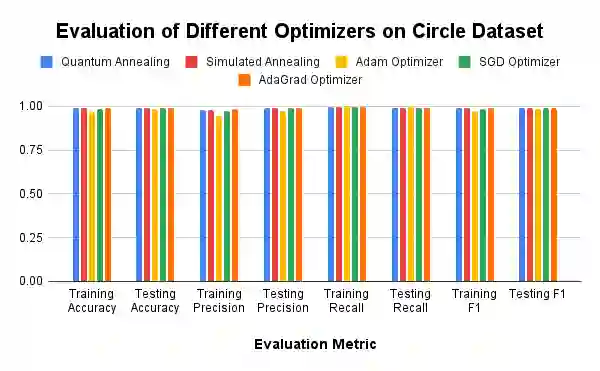
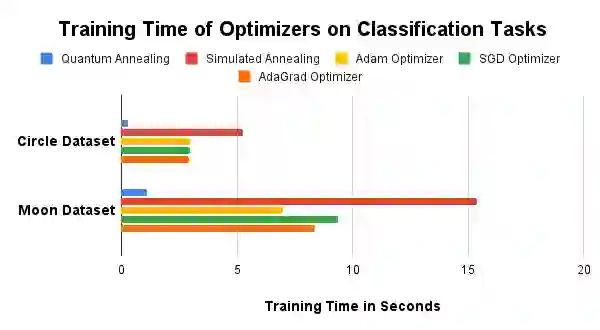
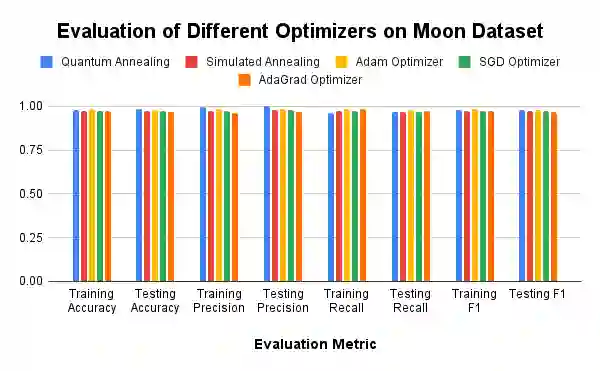
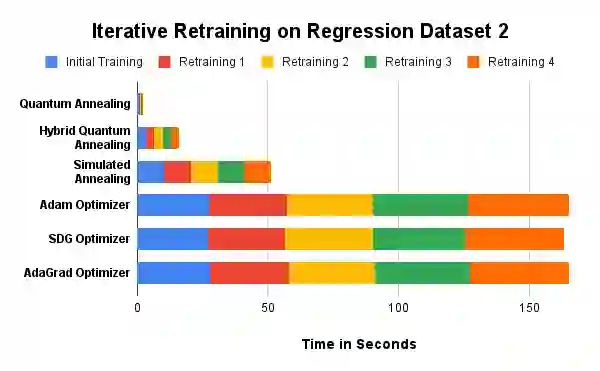
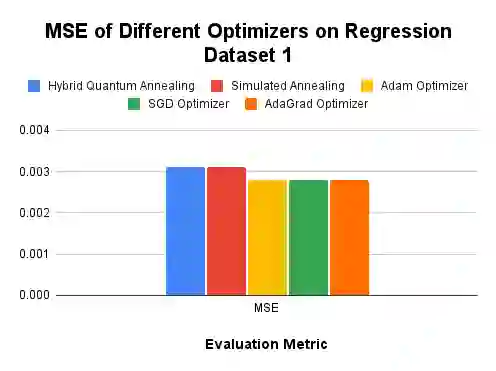
The advent of quantum computing holds the potential to revolutionize various fields by solving complex problems more efficiently than classical computers. Despite this promise, practical quantum advantage is hindered by current hardware limitations, notably the small number of qubits and high noise levels. In this study, we leverage adiabatic quantum computers to optimize Kolmogorov-Arnold Networks, a powerful neural network architecture for representing complex functions with minimal parameters. By modifying the network to use Bezier curves as the basis functions and formulating the optimization problem into a Quadratic Unconstrained Binary Optimization problem, we create a fixed-sized solution space, independent of the number of training samples. Our approach demonstrates sparks of quantum advantage through faster training times compared to classical optimizers such as the Adam, Stochastic Gradient Descent, Adaptive Gradient, and simulated annealing. Additionally, we introduce a novel rapid retraining capability, enabling the network to be retrained with new data without reprocessing old samples, thus enhancing learning efficiency in dynamic environments. Experimental results on initial training of classification and regression tasks validate the efficacy of our approach, showcasing significant speedups and comparable performance to classical methods. While experiments on retraining demonstrate a sixty times speed up using adiabatic quantum computing based optimization compared to that of the gradient descent based optimizers, with theoretical models allowing this speed up to be even larger! Our findings suggest that with further advancements in quantum hardware and algorithm optimization, quantum-optimized machine learning models could have broad applications across various domains, with initial focus on rapid retraining.
翻译:暂无翻译