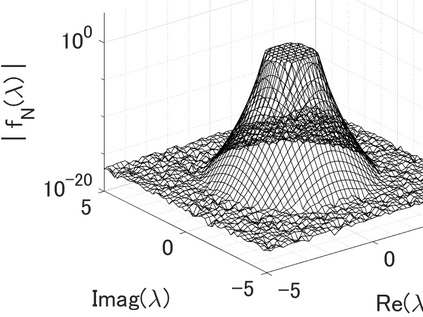
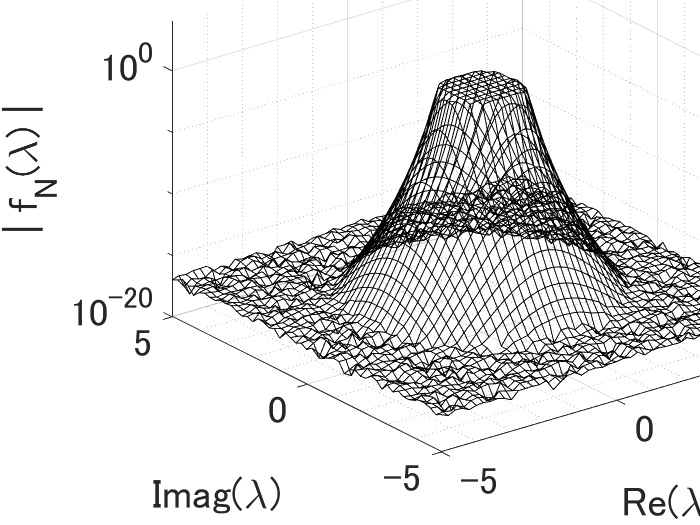
This paper considers computing partial eigenpairs of differential eigenvalue problems (DEPs) such that eigenvalues are in a certain region on the complex plane. Recently, based on a "solve-then-discretize" paradigm, an operator analogue of the FEAST method has been proposed for DEPs without discretization of the coefficient operators. Compared to conventional "discretize-then-solve" approaches that discretize the operators and solve the resulting matrix problem, the operator analogue of FEAST exhibits much higher accuracy; however, it involves solving a large number of ordinary differential equations (ODEs). In this paper, to reduce the computational costs, we propose operation analogues of Sakurai-Sugiura-type complex moment-based eigensolvers for DEPs using higher-order complex moments and analyze the error bound of the proposed methods. We show that the number of ODEs to be solved can be reduced by a factor of the degree of complex moments without degrading accuracy, which is verified by numerical results. Numerical results demonstrate that the proposed methods are over five times faster compared with the operator analogue of FEAST for several DEPs while maintaining almost the same high accuracy. This study is expected to promote the "solve-then-discretize" paradigm for solving DEPs and contribute to faster and more accurate solutions in real-world applications.
翻译:本文考虑的是,对不同二元值问题进行部分计算,使二元值出现在复杂平面上的某个区域。 最近,根据“溶解-现分解”的范式,提议对二元值处理器采用FTRET方法的操作者模拟,而没有将系数操作者分开处理。与传统的“分解-现解”方法相比,将操作者分离并解决由此产生的矩阵问题,FTRES的操作者模拟显示的精确度要高得多;然而,它涉及解决大量普通差分方程(ODEs)的问题。在本文中,为了降低计算成本,我们提议对二元值处理器采用“解析-现分解-现解”的类似操作器。与传统的“分解-现-现解”方法相比,将操作者分离并解决由此造成的矩阵问题的方法数量可以减少一个复杂度的系数,而不会降低准确度,这一点通过数字结果得到验证。 数字结果表明,为了降低计算成本,为了降低计算成本,我们提议的方法的精确性结果表明,Skuurai- Sugial结果表明,对于D-deal lial comal disal disal dispeal disal dis demod for the slipeut the pre pal democial democial democial develut develuts puts disal develuts to made to made to made to made to made to made to madefrvipeuts puts pre 也几乎几乎几乎几乎近五比比前几度研究。