Markov $α$-Potential Games: Equilibrium Approximation and Regret Analysis

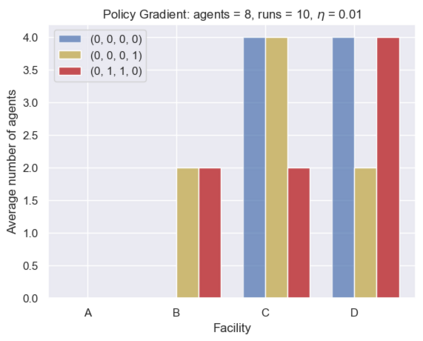
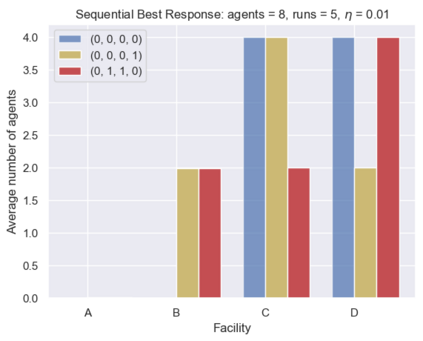
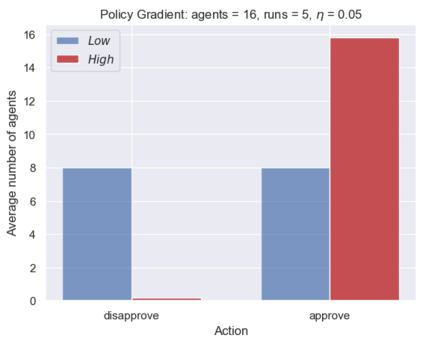
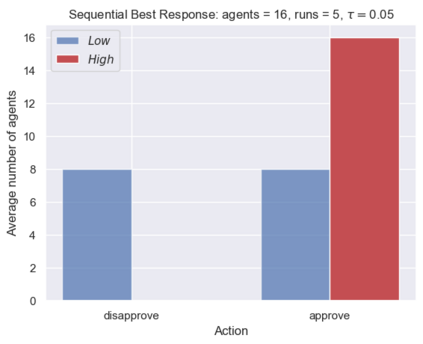
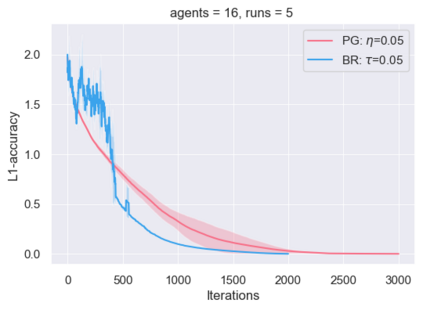
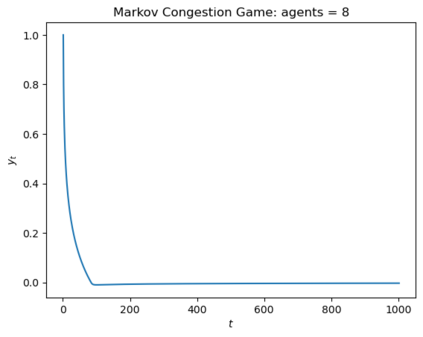
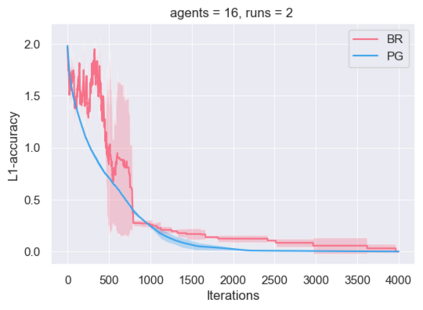
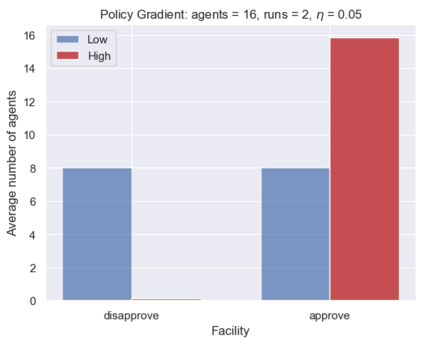
This paper proposes a new framework to study multi-agent interactions in Markov games: Markov $\alpha$-potential game. A game is called Markov $\alpha$-potential game if there exists a Markov potential game such that the pairwise difference between the change of a player's value function under a unilateral policy deviation in the Markov game and Markov potential game can be bounded by $\alpha$. As a special case, Markov potential games are Markov $\alpha$-potential games with $\alpha=0$. The dependence of $\alpha$ on the game parameters is also explicitly characterized in two classes of games that are practically-relevant: Markov congestion games and the perturbed Markov team games. For general Markov games, an optimization-based approach is introduced which can compute a Markov potential game which is closest to the given game in terms of $\alpha$. This approach can also be used to verify whether a game is a Markov potential game, and provide a candidate potential function. Two algorithms -- the projected gradient-ascent algorithm and the {sequential maximum one-stage improvement} -- are provided to approximate the stationary Nash equilibrium in Markov $\alpha$-potential games and the corresponding Nash-regret analysis is presented. The numerical experiments demonstrate that simple algorithms are capable of finding approximate equilibrium in Markov $\alpha$-potential games.