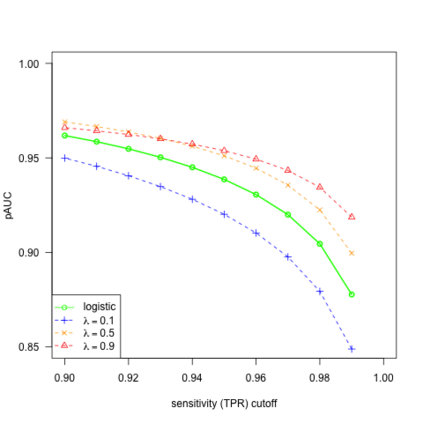
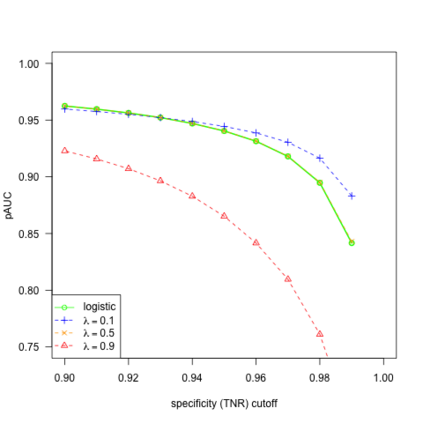
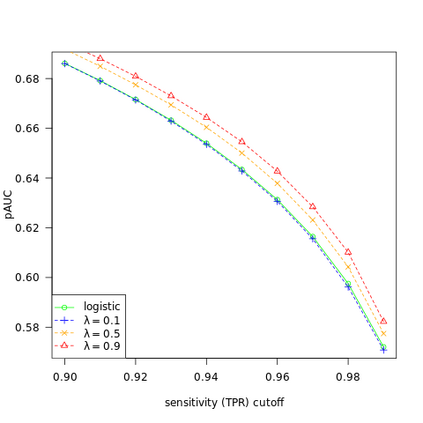
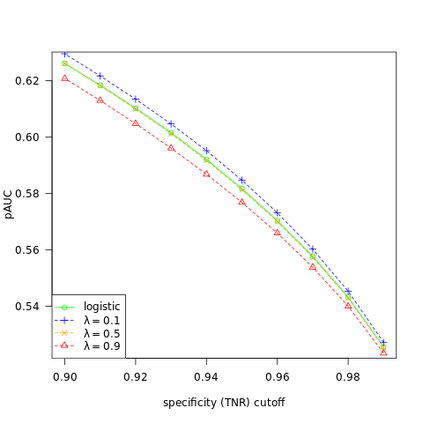
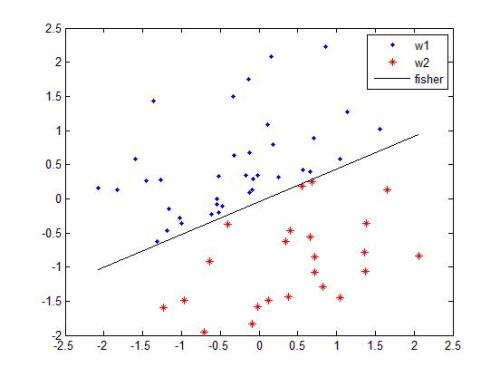
We study the behavior of linear discriminant functions for binary classification in the infinite-imbalance limit, where the sample size of one class grows without bound while the sample size of the other remains fixed. The coefficients of the classifier minimize an expected loss specified through a weight function. We show that for a broad class of weight functions, the intercept diverges but the rest of the coefficient vector has a finite limit under infinite imbalance, extending prior work on logistic regression. The limit depends on the left tail of the weight function, for which we distinguish three cases: bounded, asymptotically polynomial, and asymptotically exponential. The limiting coefficient vectors reflect robustness or conservatism properties in the sense that they optimize against certain worst-case alternatives. In the bounded and polynomial cases, the limit is equivalent to an implicit choice of upsampling distribution for the minority class. We apply these ideas in a credit risk setting, with particular emphasis on performance in the high-sensitivity and high-specificity regions.
翻译:在无限平衡限度内,一个类的样本规模不受约束地增长,而另一个类的样本规模保持不变。分类器的系数将一个重量函数指定的预期损失最小化。我们表明,对于一个广泛的重量函数类别,截取的参数有差异,但系数矢量的其余部分则在无限不平衡下有一定的限度,延长了先前的后勤回归工作。这一限制取决于重量函数的左尾,为此我们区分了三种情况:受约束的、无症状的多元性的和无症状的指数性。限制的系数矢量反映了稳健或保守的特性,即它们针对某些最坏的替代物优化。在受约束的和多元的案例中,这一限度相当于对少数类的扩大分布的隐性选择。我们在信用风险设置中应用这些想法,特别侧重于高敏感度和高特定区域的性能。