Least Squares Estimation of a Quasiconvex Regression Function

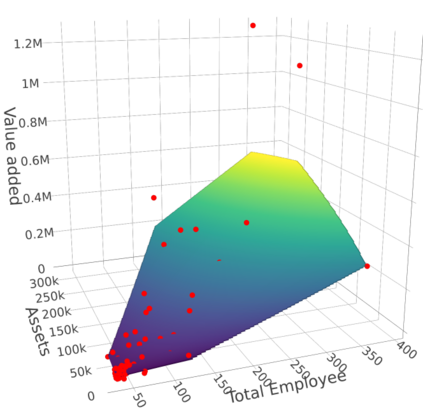
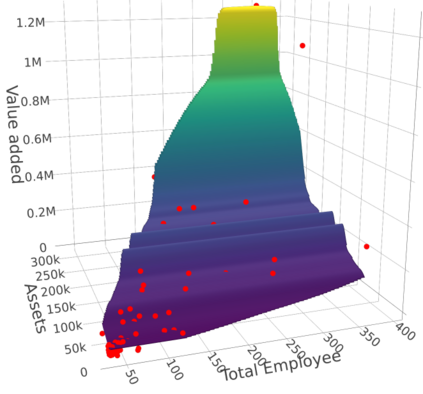
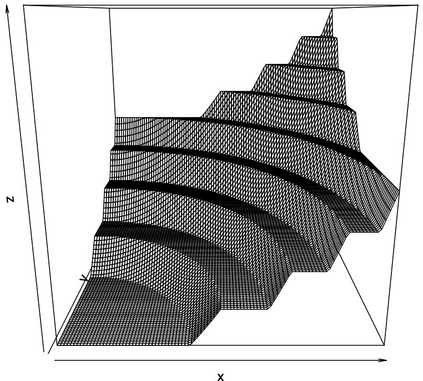
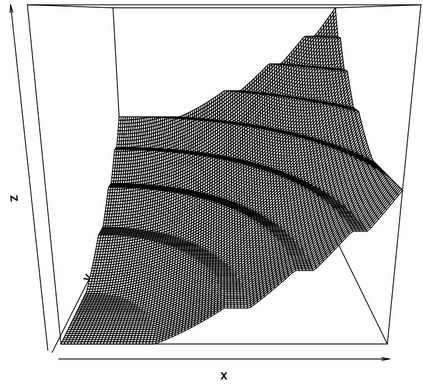
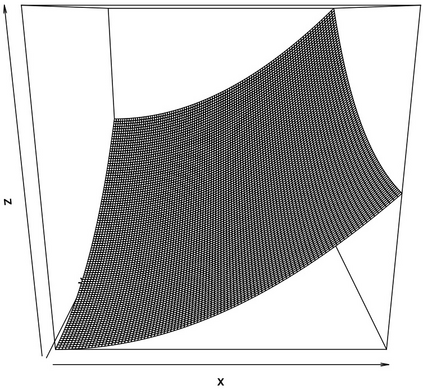
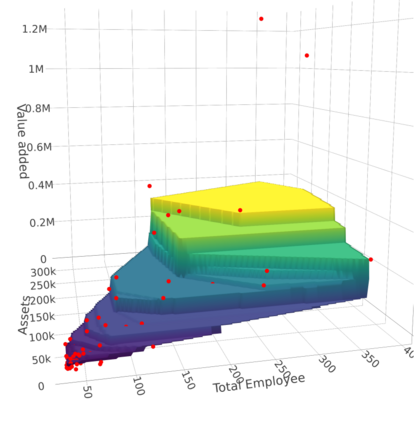
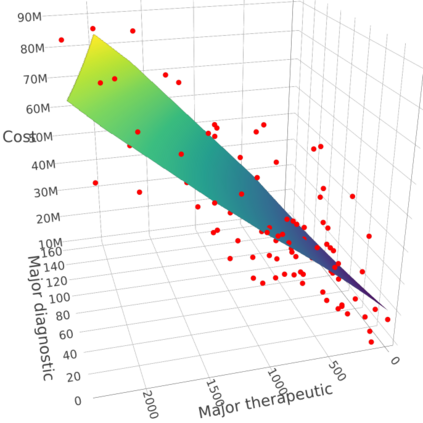
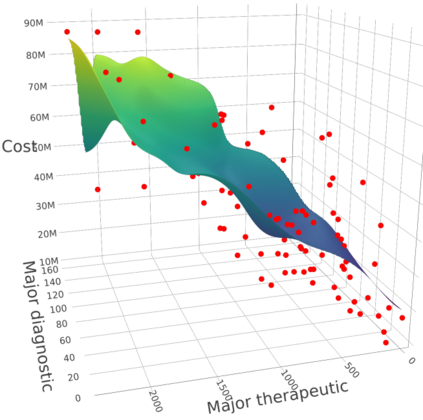
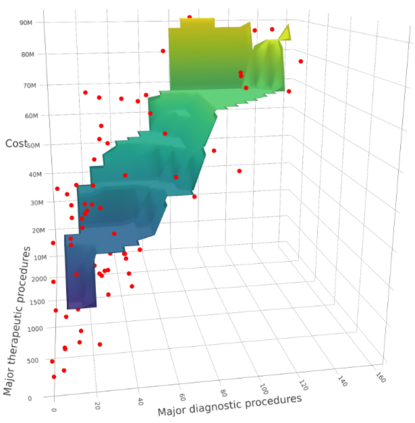
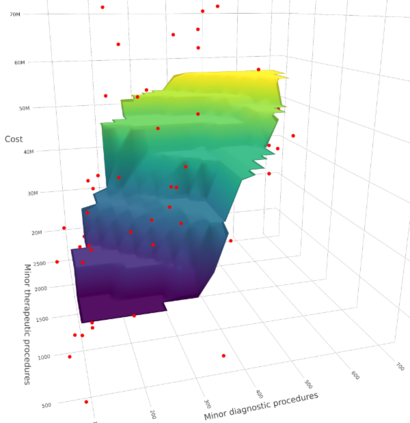
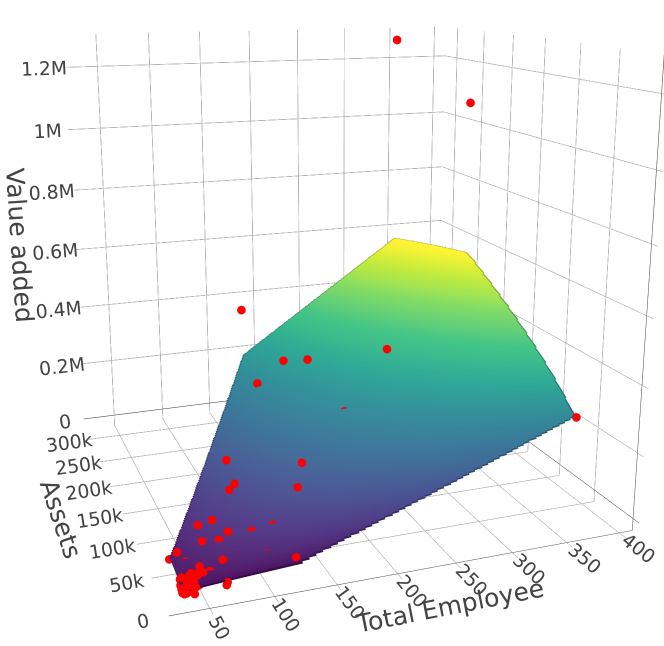
We develop a new approach for the estimation of a multivariate function based on the economic axioms of quasiconvexity (and monotonicity). On the computational side, we prove the existence of the quasiconvex constrained least squares estimator (LSE) and provide a characterization of the function space to compute the LSE via a mixed integer quadratic programme. On the theoretical side, we provide finite sample risk bounds for the LSE via a sharp oracle inequality. Our results allow for errors to depend on the covariates and to have only two finite moments. We illustrate the superior performance of the LSE against some competing estimators via simulation. Finally, we use the LSE to estimate the production function for the Japanese plywood industry and the cost function for hospitals across the US.