Stochastic Inverse Reinforcement Learning

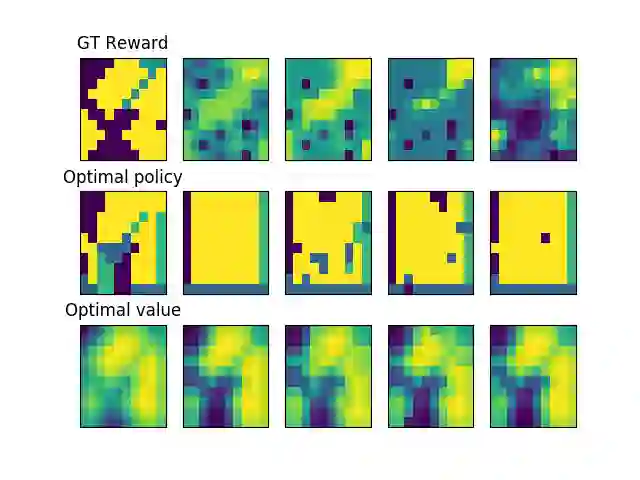
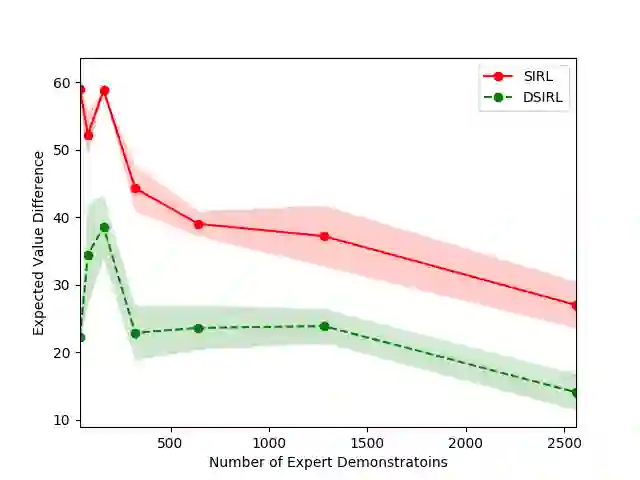
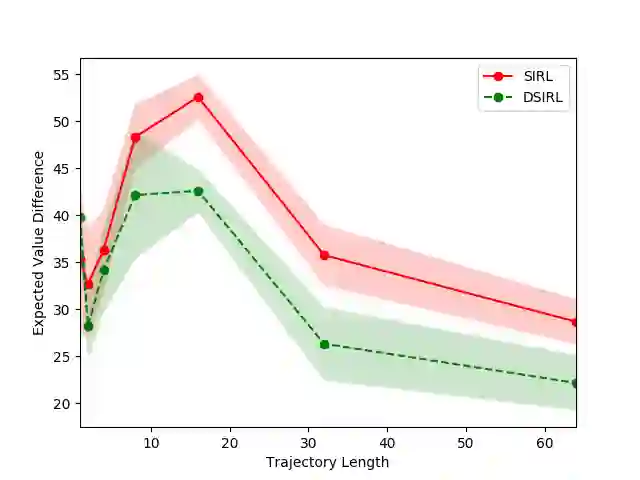
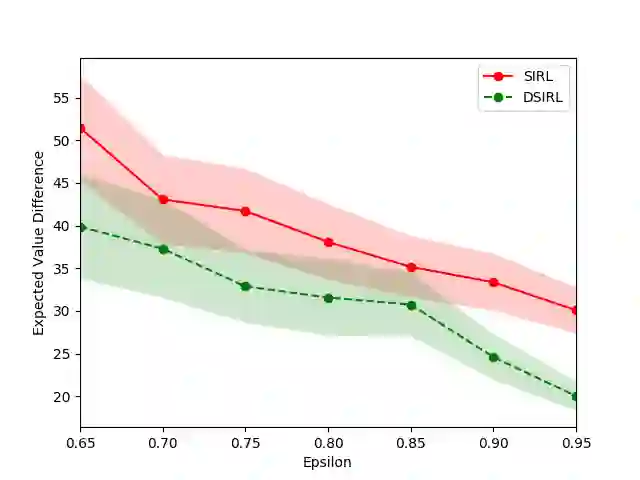
The goal of the inverse reinforcement learning (IRL) problem is to recover the reward functions from expert demonstrations. However, the IRL problem like any ill-posed inverse problem suffers the congenital defect that the policy may be optimal for many reward functions, and expert demonstrations may be optimal for many policies. In this work, we generalize the IRL problem to a well-posed expectation optimization problem stochastic inverse reinforcement learning (SIRL) to recover the probability distribution over reward functions. We adopt the Monte Carlo expectation-maximization (MCEM) method to estimate the parameter of the probability distribution as the first solution to the SIRL problem. The solution is succinct, robust, and transferable for a learning task and can generate alternative solutions to the IRL problem. Through our formulation, it is possible to observe the intrinsic property of the IRL problem from a global viewpoint, and our approach achieves a considerable performance on the objectworld.