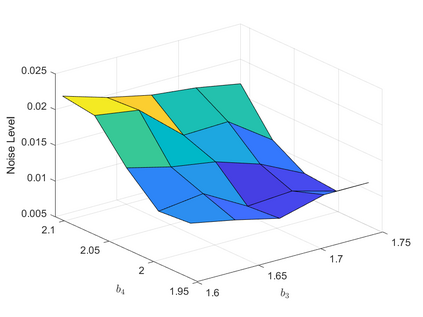
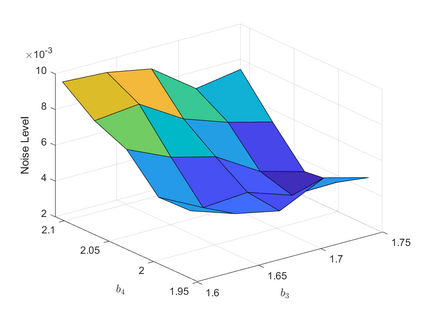
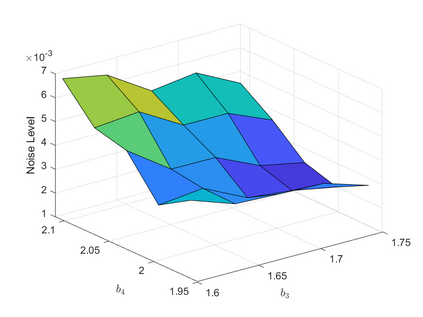
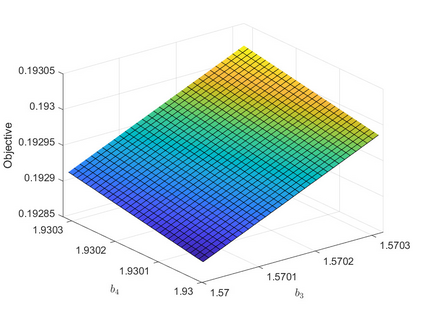
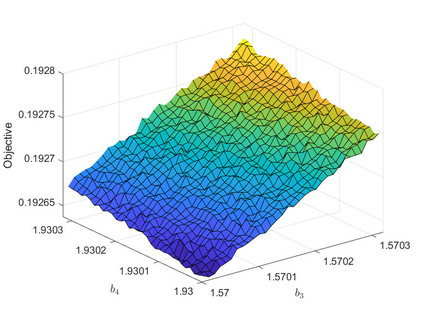
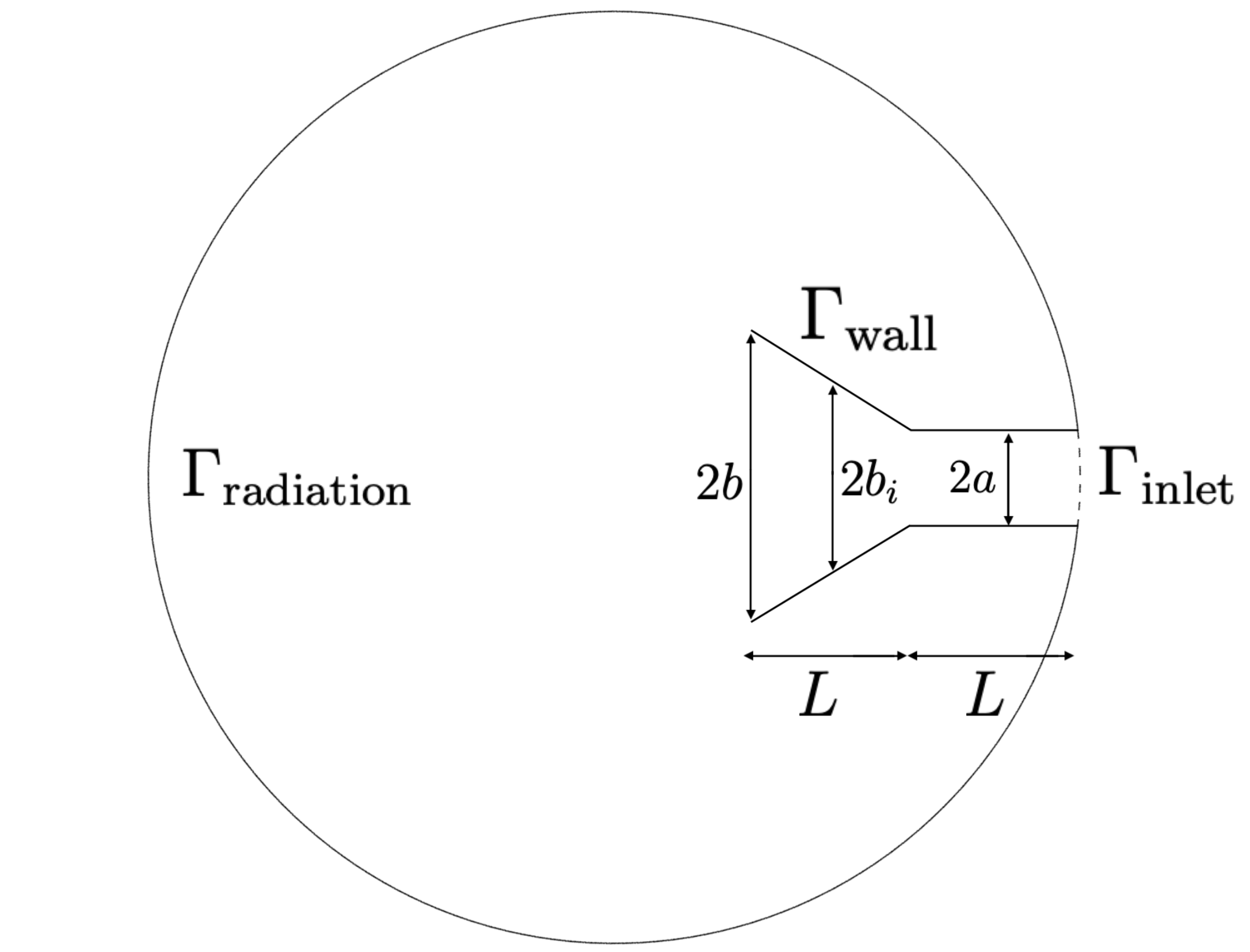
The development of nonlinear optimization algorithms capable of performing reliably in the presence of noise has garnered considerable attention lately. This paper advocates for strategies to create noise-tolerant nonlinear optimization algorithms by adapting classical deterministic methods. These adaptations follow certain design guidelines described here, which make use of estimates of the noise level in the problem. The application of our methodology is illustrated by the development of a line search gradient projection method, which is tested on an engineering design problem. It is shown that a new self-calibrated line search and noise-aware finite-difference techniques are effective even in the high noise regime. Numerical experiments investigate the resiliency of key algorithmic components. A convergence analysis of the line search gradient projection method establishes convergence to a neighborhood of the solution.
翻译:暂无翻译