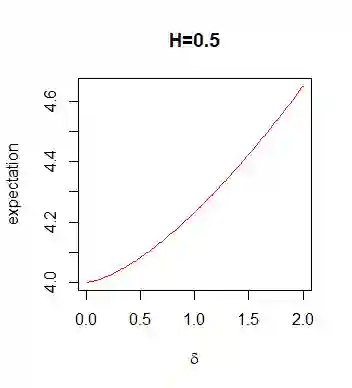
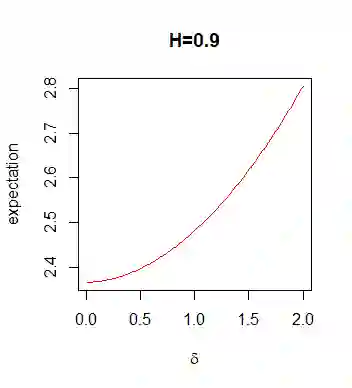
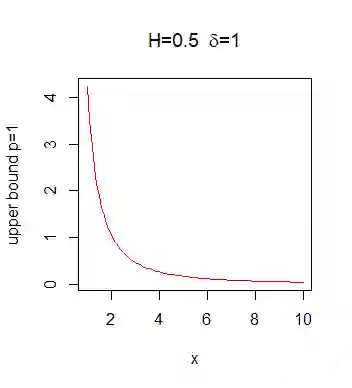
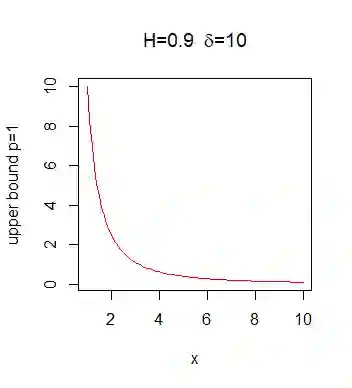
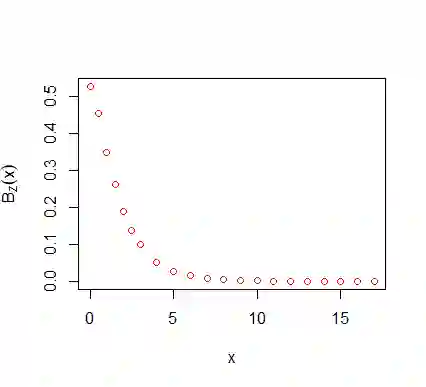
For fractional Brownian motion with Hurst parameter H the Berman constant is defined. In this paper we consider a general random field (rf) Z that is a spectral rf of some stationary max-stable rf X and derive the properties of the corresponding Berman functions. In particular, we show that Berman functions can be approximated by the corresponding discrete ones and derive interesting representations of those functions which are of interest for Monte Carlo simulations, which are presented in this article.
翻译：对于带有赫斯特参数H的分数布朗运动,定义了伯曼常数。在本文件中,我们考虑的是普通随机字段(rf) Z,它是某种固定最大稳定的 rf X 的光谱 rf, 并得出相应的伯曼函数的属性。特别是,我们表明,伯曼函数可以与相应的离散函数相近,并得出对蒙特卡洛模拟感兴趣的那些函数的有趣的表示,本篇文章中介绍了这些函数。
相关内容
Arxiv
0+阅读 · 2023年1月1日
Arxiv
0+阅读 · 2022年12月30日
Arxiv
0+阅读 · 2022年12月30日
Arxiv
0+阅读 · 2022年12月28日
Arxiv
18+阅读 · 2022年11月7日
相关VIP内容
相关资讯
相关论文
Arxiv
0+阅读 · 2023年1月1日
Arxiv
0+阅读 · 2022年12月30日
Arxiv
0+阅读 · 2022年12月30日
Arxiv
0+阅读 · 2022年12月28日
Arxiv
18+阅读 · 2022年11月7日
微信扫码咨询专知VIP会员