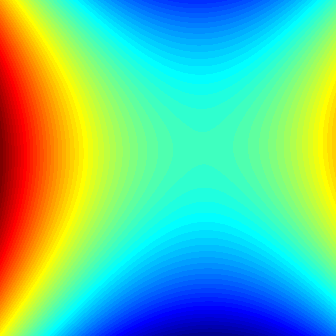
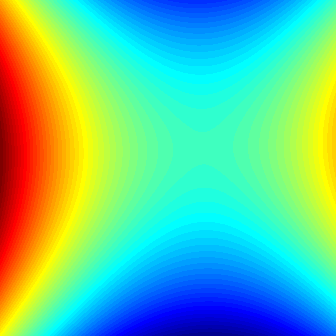
Finding discriminant functions of minimum risk binary classification systems is a novel geometric locus problem -- which requires solving a system of fundamental locus equations of binary classification -- subject to deep-seated statistical laws. We show that a discriminant function of a minimum risk binary classification system is the solution of a locus equation that represents the geometric locus of the decision boundary of the system, wherein the discriminant function is connected to the decision boundary by an exclusive principal eigen-coordinate system -- at which point the discriminant function is represented by a geometric locus of a novel principal eigenaxis -- structured as a dual locus of likelihood components and principal eigenaxis components. We demonstrate that a minimum risk binary classification system acts to jointly minimize its eigenenergy and risk by locating a point of equilibrium, at which point critical minimum eigenenergies exhibited by the system are symmetrically concentrated in such a manner that the novel principal eigenaxis of the system exhibits symmetrical dimensions and densities, so that counteracting and opposing forces and influences of the system are symmetrically balanced with each other -- about the geometric center of the locus of the novel principal eigenaxis -- whereon the statistical fulcrum of the system is located. Thereby, a minimum risk binary classification system satisfies a state of statistical equilibrium -- so that the total allowed eigenenergy and the expected risk exhibited by the system are jointly minimized within the decision space of the system -- at which point the system exhibits the minimum probability of classification error.
翻译:最低风险二进制分类系统具有不同功能,这是一个新的几何轨道问题 -- -- 需要解决二进制分类基本轨迹的系统 -- -- 需要遵循深层次的统计法。我们显示,最低风险二进制分类系统具有不同功能,这是代表系统决定界限几何点的轨迹方程式的解决方案,在这一点上,该系统显示的临界最小电子内脏功能通过一个排他性的主要双元坐标系统与决定界限相连 -- -- 在这个点上,这个系统的新颖的正对等功能代表着一个全新的主要电子等离子体的几何点 -- -- 其结构结构是概率组成部分和主要电子异性成分的双重中心。 我们显示,一个最低风险二进制分类系统通过定位一个平衡点来联合尽量减少其电子能量和风险。 在这个点上,该系统所展示的关键最低电子内最小电子内积分数功能的精度功能集中到一个新式的正数和对数系统内部的精确度,其精确度的精确度系统在其中的精确度上,其精确度的精确度系统在每一统计中心,其统计的精确度的精确度的准确度上是统计系统的精确度系统。