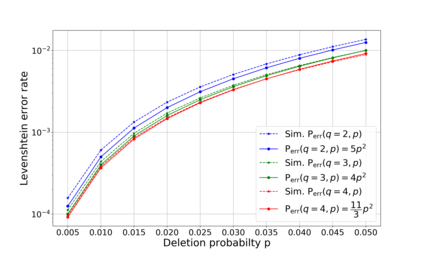
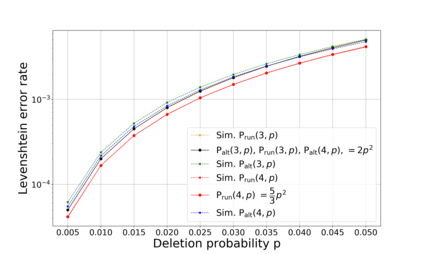
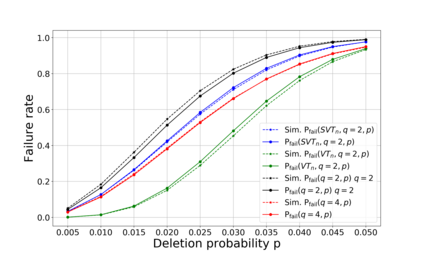
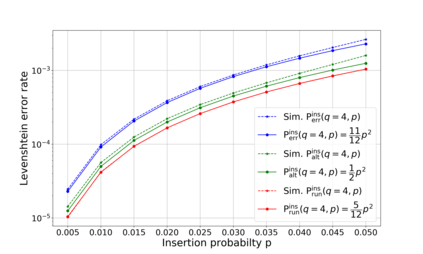
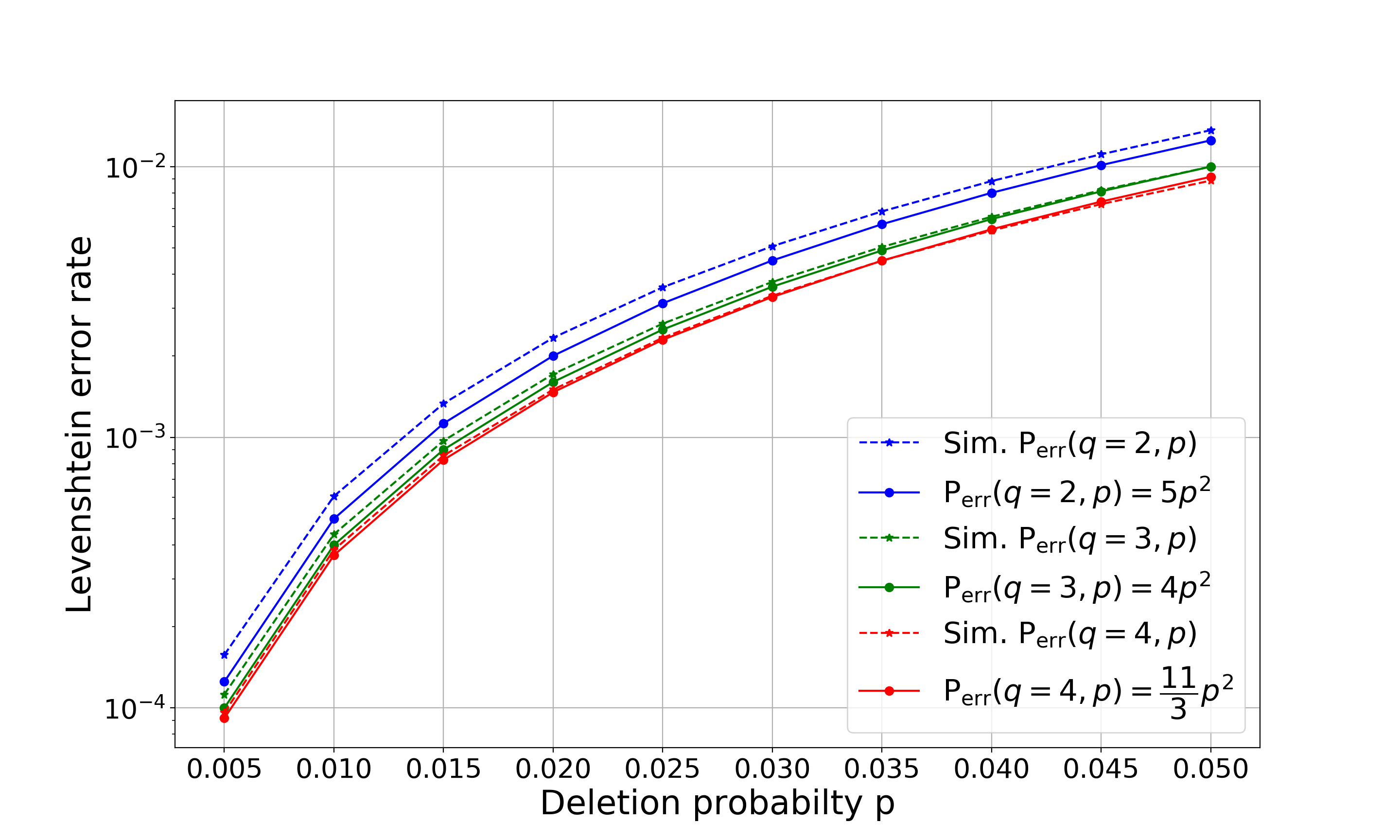
This paper tackles two problems that are relevant to coding for insertions and deletions. These problems are motivated by several applications, among them is reconstructing strands in DNA-based storage systems. Under this paradigm, a word is transmitted over some fixed number of identical independent channels and the goal of the decoder is to output the transmitted word or some close approximation of it. The first part of this paper studies the deletion channel that deletes a symbol with some fixed probability $p$, while focusing on two instances of this channel. Since operating the maximum likelihood (ML) decoder in this case is computationally unfeasible, we study a slightly degraded version of this decoder for two channels and its expected normalized distance. We identify the dominant error patterns and based on these observations, it is derived that the expected normalized distance of the degraded ML decoder is roughly $\frac{3q-1}{q-1}p^2$, when the transmitted word is any $q$-ary sequence and $p$ is the channel's deletion probability. We also study the cases when the transmitted word belongs to the Varshamov Tenengolts (VT) code or the shifted VT code. Additionally, the insertion channel is studied as well as the case of two insertion channels. These theoretical results are verified by corresponding simulations. The second part of the paper studies optimal decoding for a special case of the deletion channel, the $k$-deletion channel, which deletes exactly $k$ symbols of the transmitted word uniformly at random. In this part, the goal is to understand how an optimal decoder operates in order to minimize the expected normalized distance. A full characterization of an efficient optimal decoder for this setup, referred to as the maximum likelihood* (ML*) decoder, is given for a channel that deletes one or two symbols.
翻译:本文的第一部分研究与插入和删除编码相关的两个问题。 这些问题是由多个应用程序引发的, 其中包括重建基于DNA的存储系统中的解码线。 在此范式下, 一个单词通过一些相同独立频道的固定数量传递, 解码器的目标是输出所传输的单词或某近似值。 本文的第一部分研究删除频道, 以某种固定概率删除一个符号, 并关注此频道的两种情况。 由于在此情况下操作的最大可能性( ML) 传输的解码符是计算不可行的, 我们为两个频道的解码值重建一个稍微退化的版本。 我们根据这些观察, 确定一个主要错误模式, 并推导出, 退化的 ML decoder 解码器的预期正常距离大约是$frac{3q-1qQ-1}p2$, 当传输的单词是删除任何美元, 和 $polp$是频道的删除概率。 当传输单词属于 Varhamder* 的解码属于 Varhamder Teal 的解算法部分时, 的解算算算算法, 。 在两个解算法中, 的解算法中, 的解算算法是这个解算法, 。 的解解的解算法, 。