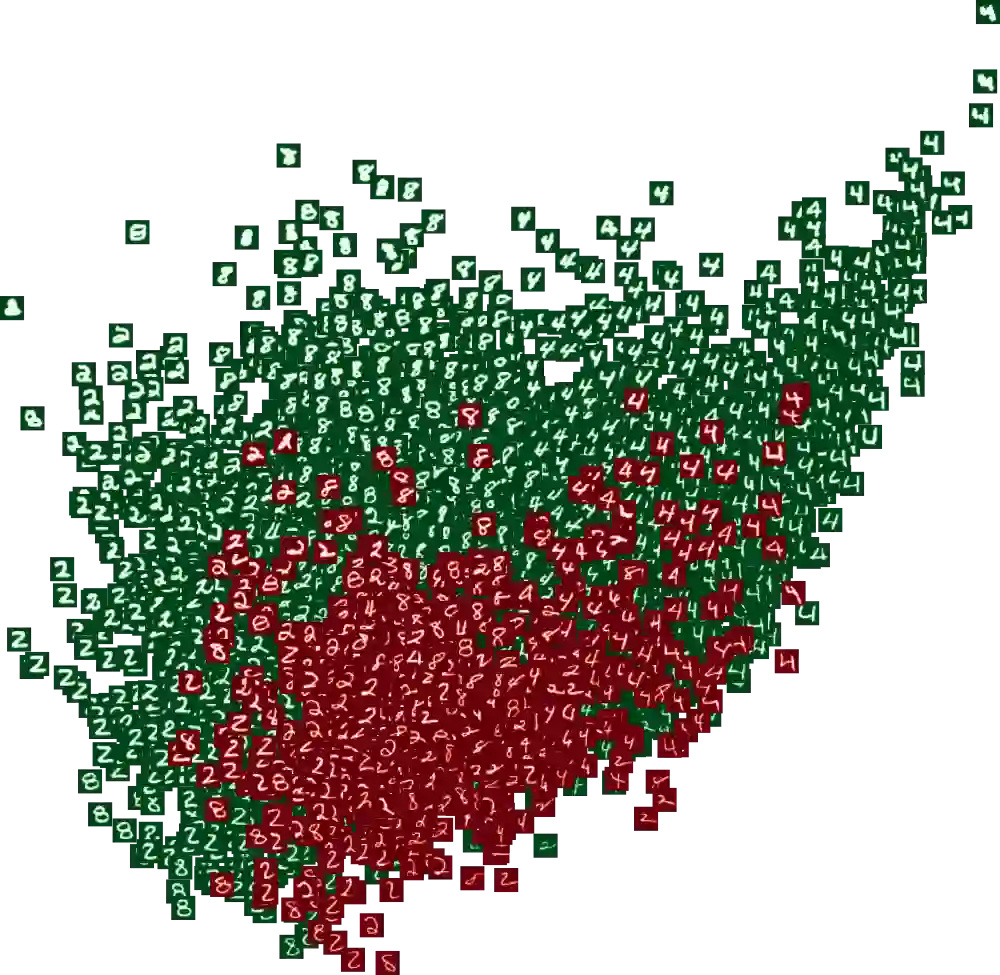
The encoder network of an autoencoder is an approximation of the nearest point projection onto the manifold spanned by the decoder. A concern with this approximation is that, while the output of the encoder is always unique, the projection can possibly have infinitely many values. This implies that the latent representations learned by the autoencoder can be misleading. Borrowing from geometric measure theory, we introduce the idea of using the reach of the manifold spanned by the decoder to determine if an optimal encoder exists for a given dataset and decoder. We develop a local generalization of this reach and propose a numerical estimator thereof. We demonstrate that this allows us to determine which observations can be expected to have a unique, and thereby trustworthy, latent representation. As our local reach estimator is differentiable, we investigate its usage as a regularizer and show that this leads to learned manifolds for which projections are more often unique than without regularization.
翻译:自动编码器编码器的编码器网络近似于对解码器所覆盖的方块的最近的点投影。 对这一近似值的担心是, 虽然编码器的输出总是独特的, 但投影可能具有无限的数值。 这意味着自动编码器所学的潜在显示方式可能会产生误导。 从几何测量理论中借用, 我们引入了使用解码器所覆盖的方块的覆盖范围来确定某个数据集和解码器是否存在最佳的编码器。 我们开发了此方块的本地概括, 并推荐了一个数字估计器。 我们证明这使我们能够确定哪些观测结果可以具有独特性, 从而具有可信任性, 潜显示我们本地的定位器是不同的, 我们用它作为常规的调节器来调查, 并显示这会导致所学到的方块图比没有正规化的要更加独特。