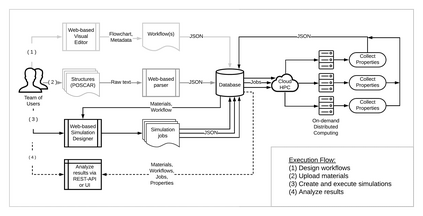
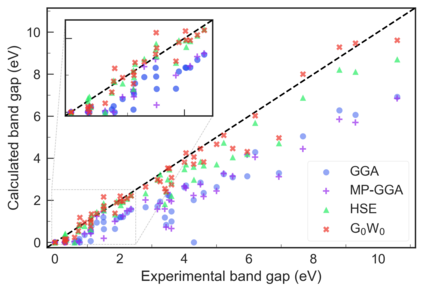
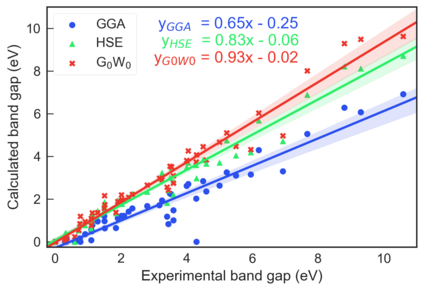
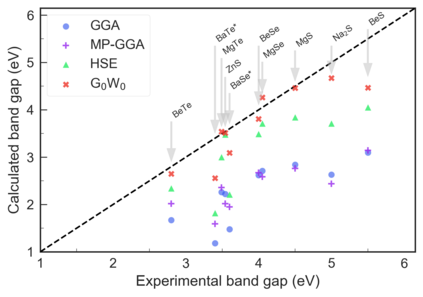
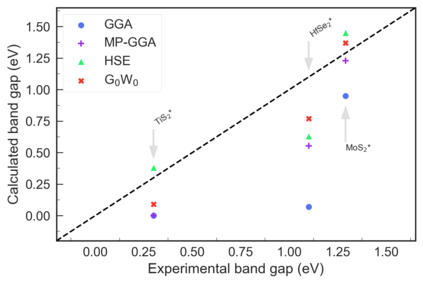
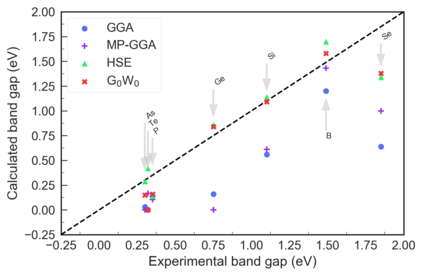
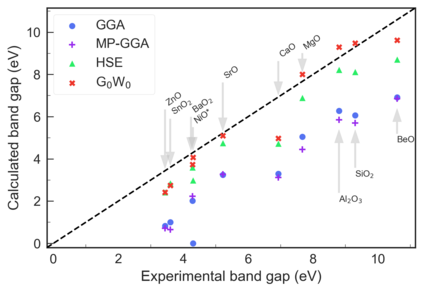
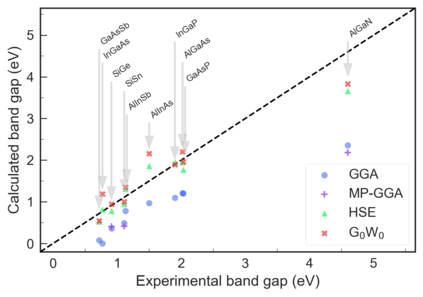
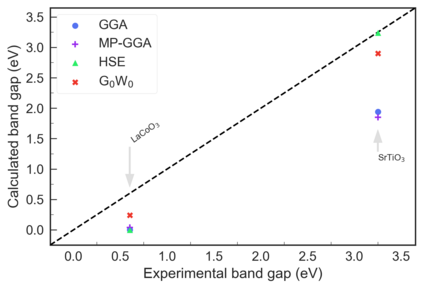
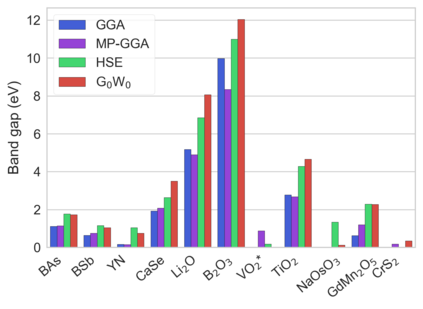
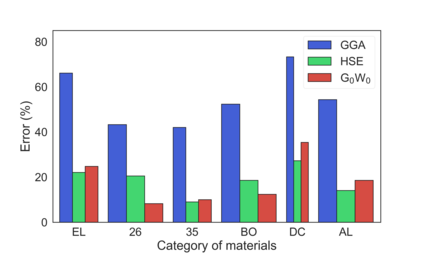
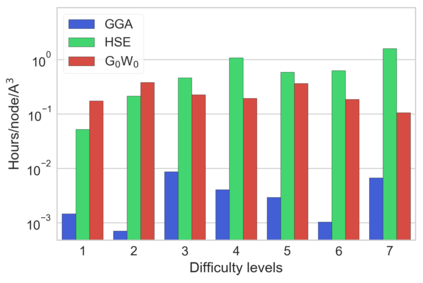
Despite multiple successful applications of high-throughput computational materials design from first principles, there is a number of factors that inhibit its future adoption. Of particular importance are limited ability to provide high fidelity in a reliable manner and limited accessibility to non-expert users. We present example applications of a novel approach, where high-fidelity first-principles simulation techniques, Density Functional Theory with Hybrid Screened Exchange (HSE) and GW approximation, are standardized and made available online in an accessible and repeatable setting. We apply this approach to extract electronic band gaps and band structures for a diverse set of 71 materials ranging from pure elements to III-V and II-VI compounds, ternary oxides and alloys. We find that for HSE and G0W0, the average relative error fits within 20%, whereas for conventional Generalized Gradient Approximation the error is 55%. For HSE we find the average calculation time on an up-to-date server centrally available from a public cloud provider to fit within 48 hours. This work provides a cost-effective, accessible and repeatable practical recipe for performing high-fidelity first-principles calculations of electronic materials in a high-throughput manner.
翻译:尽管从最初的原则中成功地应用了多种高通量计算材料设计,但有许多因素阻碍今后采用高通量计算材料,尤其重要的是,以可靠的方式提供高忠诚度的能力有限,非专家用户的可及性也有限。我们举例介绍了新颖方法的应用,即高忠度第一原则模拟技术、混合屏幕交换(HSE)和GW近似(GW)的密度功能理论是标准化的,在可访问和可重复的环境下在线提供。我们采用这种方法,为从纯元素到III-V和II-VI化合物、四氧化物和合金的71种材料抽取电子波段和带结构。我们发现,对于HSE和G0W0,平均相对误差在20%之内,而对于常规的通用精密度吸附剂(HSE)来说,误差为55%。我们发现公共云供应商在48小时内可以集中使用的更新的服务器的平均计算时间。这项工作为进行高端高端电子材料的高端计算提供了成本、易懂和可重复的实际食谱。
相关内容
Material Design Guidelines