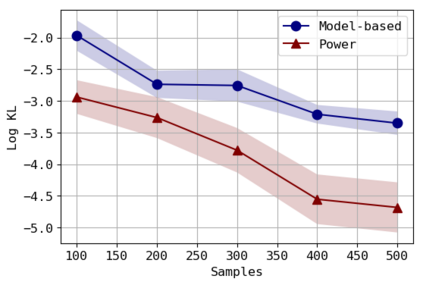
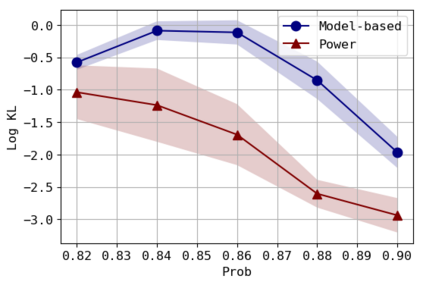
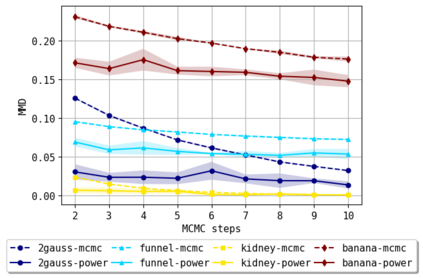
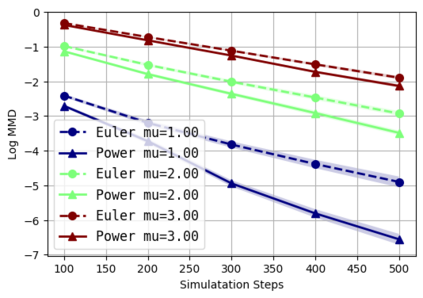
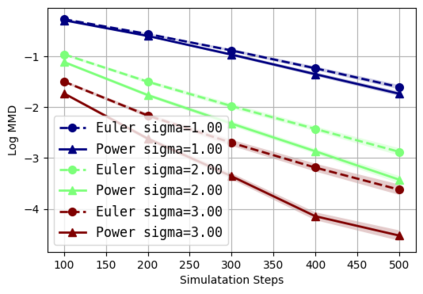
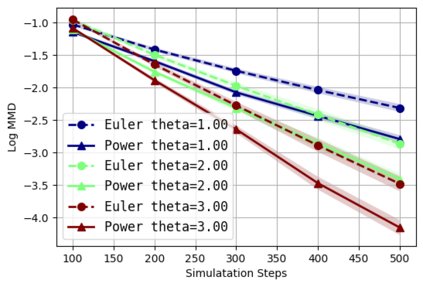
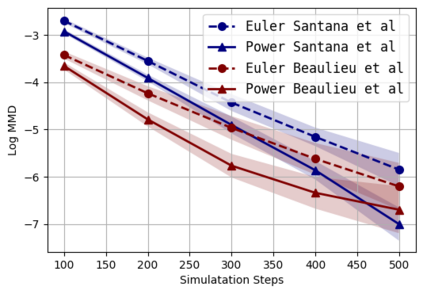
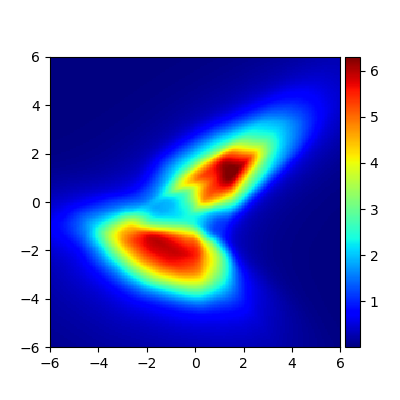
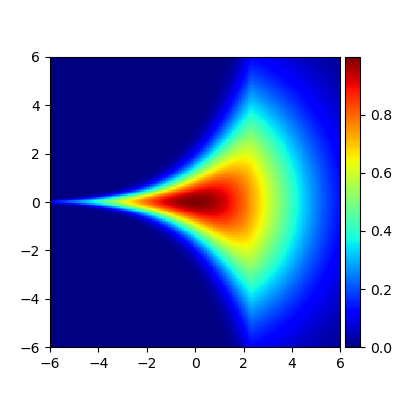
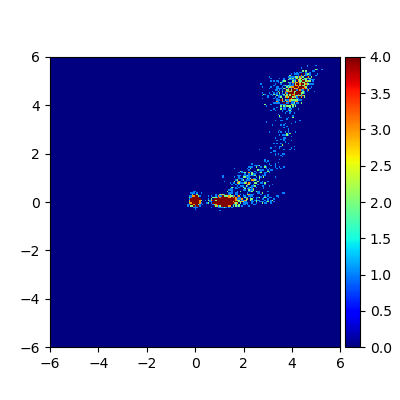
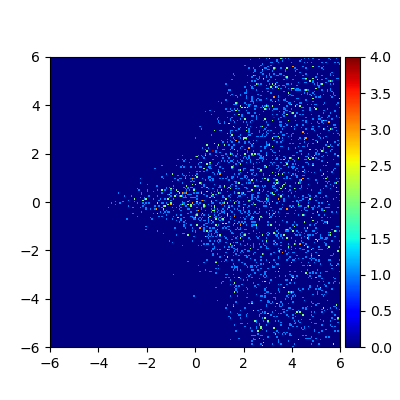
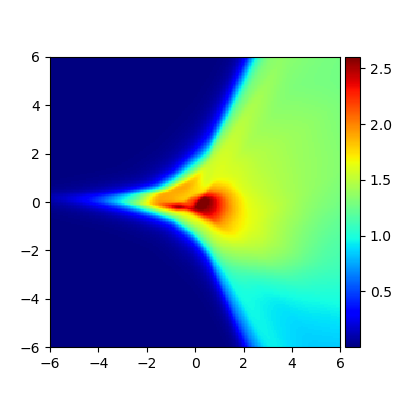
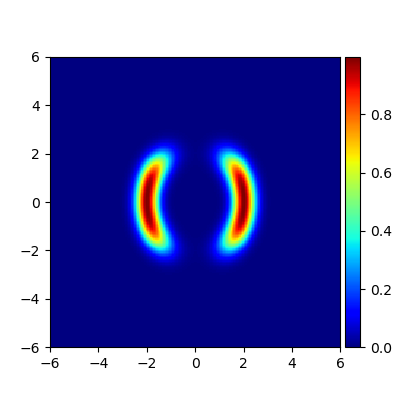
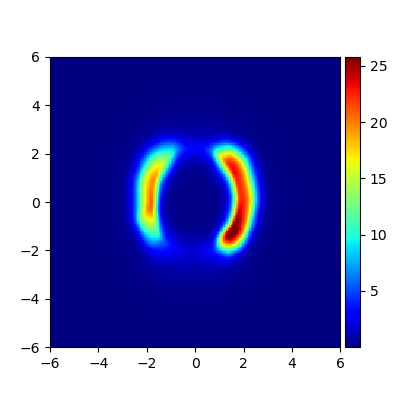
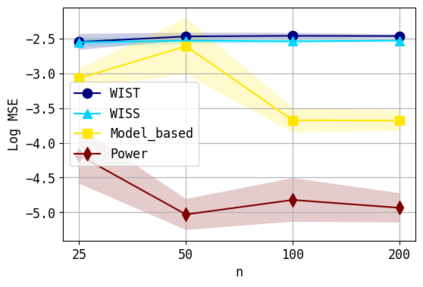
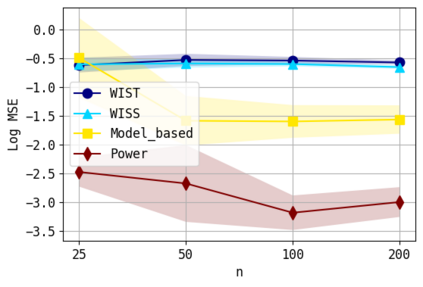
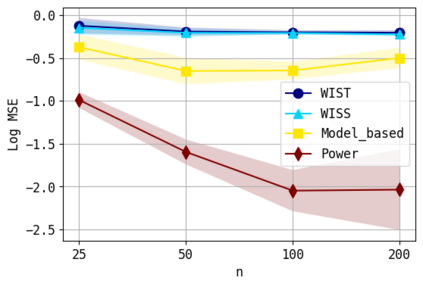
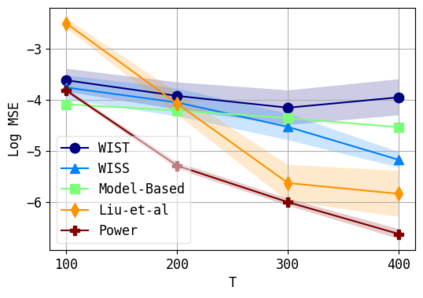
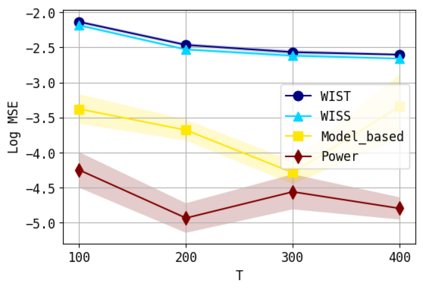
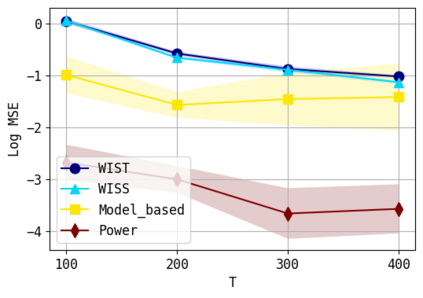
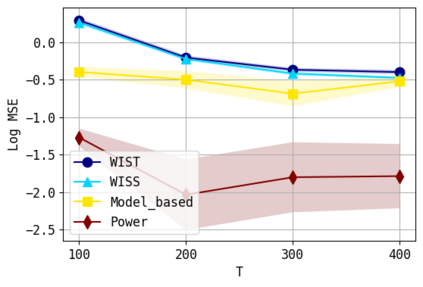
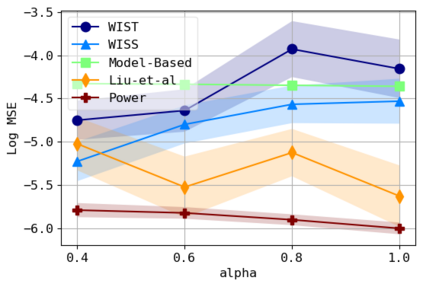
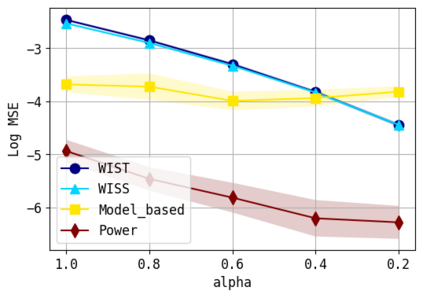
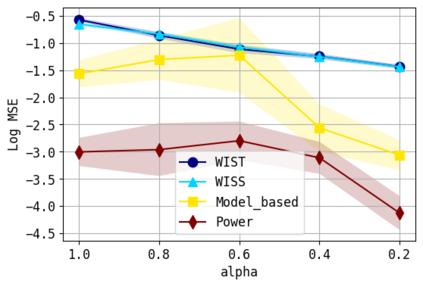
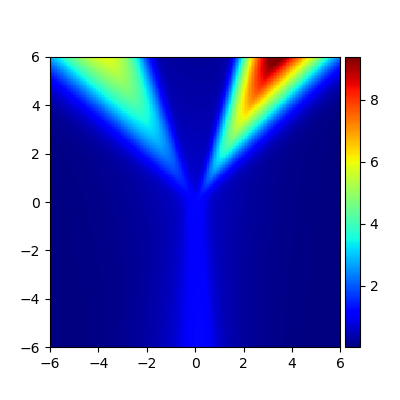
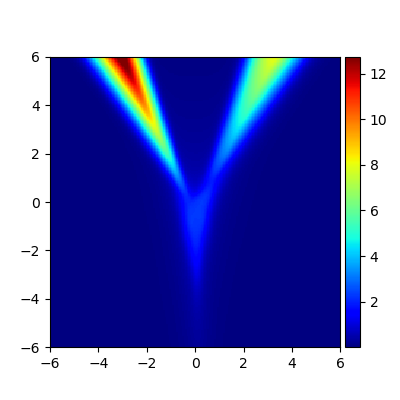
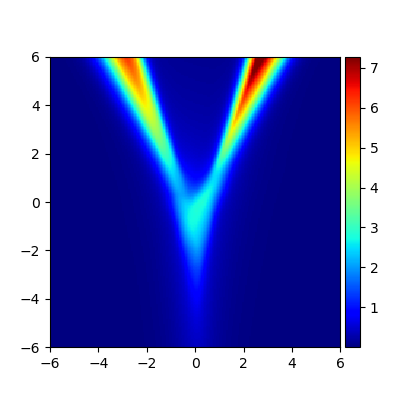
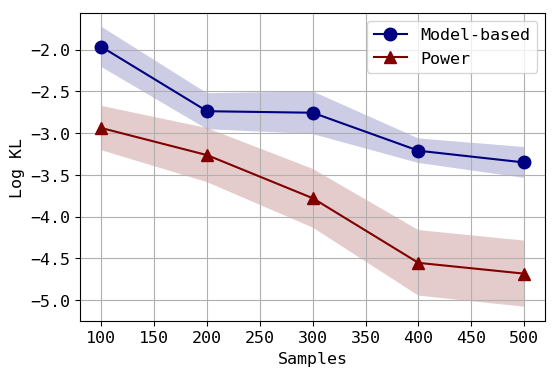
We consider the problem of approximating the stationary distribution of an ergodic Markov chain given a set of sampled transitions. Classical simulation-based approaches assume access to the underlying process so that trajectories of sufficient length can be gathered to approximate stationary sampling. Instead, we consider an alternative setting where a fixed set of transitions has been collected beforehand, by a separate, possibly unknown procedure. The goal is still to estimate properties of the stationary distribution, but without additional access to the underlying system. We propose a consistent estimator that is based on recovering a correction ratio function over the given data. In particular, we develop a variational power method (VPM) that provides provably consistent estimates under general conditions. In addition to unifying a number of existing approaches from different subfields, we also find that VPM yields significantly better estimates across a range of problems, including queueing, stochastic differential equations, post-processing MCMC, and off-policy evaluation.
翻译:我们认为,鉴于一系列抽样的过渡情况,使用典型模拟法假设可以进入基本过程,以便收集足够长的轨迹,以接近固定的抽样;相反,我们考虑一种替代环境,即事先通过单独、可能不为人知的程序收集一套固定的过渡情况;目的仍然是估计固定分布的特性,但又不能额外进入基本系统;我们提议一个一致的估测器,其依据是恢复对给定数据的校正比率功能;特别是,我们开发一种可变功率法,在一般条件下提供可变一致的估计数;除了统一不同子领域现有的若干办法外,我们还发现,VPM在一系列问题上得出了更好的估计,包括排队、分解式方程式、后处理MC以及非政策评价。