Adaptive Optimal Shrinkage of Singular Values under Colored and Dependent Noise

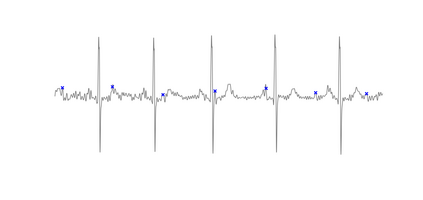
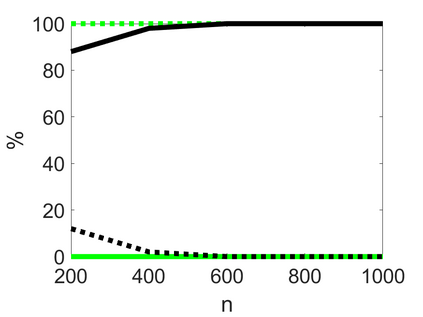
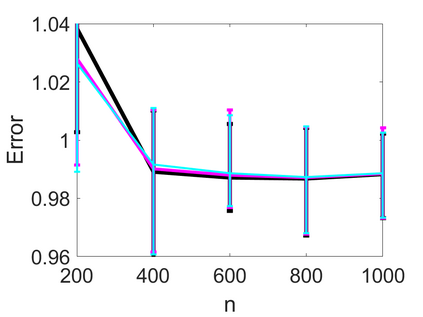
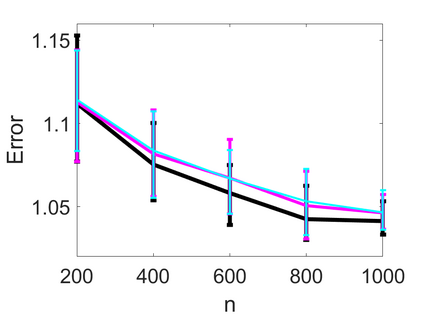
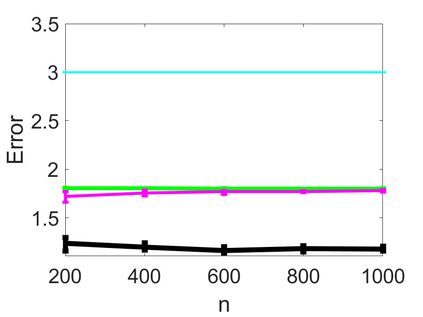
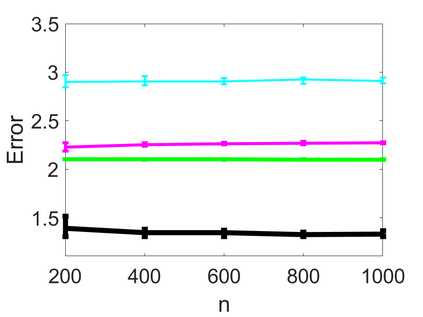
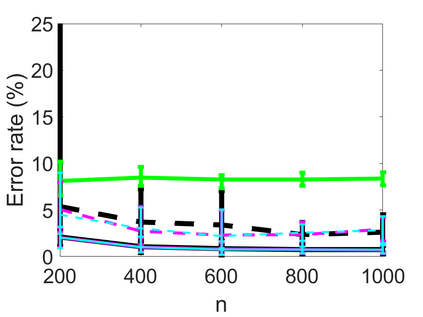
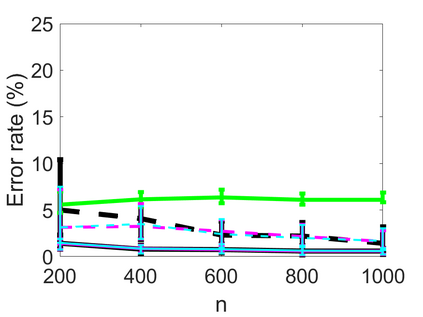
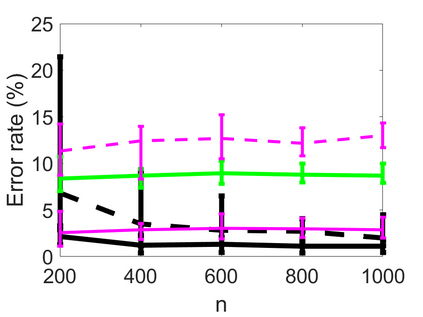
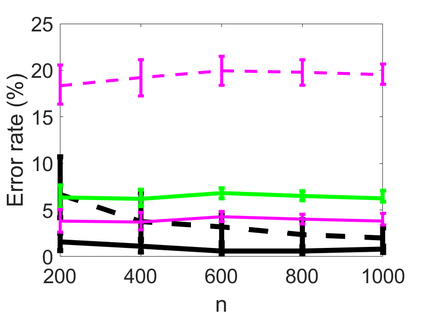
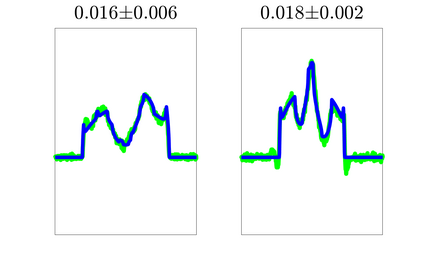
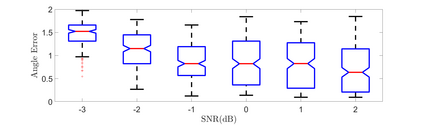
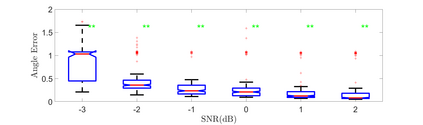
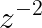We propose an adaptive optimal shrinkage algorithm with a rank estimation method for matrix denoising in the presence of high-dimensional colored and dependent noise (separable covariance). The algorithm does not depend on estimating the color and dependence structure of the noise. On the theoretical side, we study the asymptotic behavior of outlier singular values and singular vectors of the associated random matrix with a convergence rate, and apply these results to analyze the proposed adaptive optimal shrinkage algorithm and rank estimation. On the application side, we carry out simulations to demonstrate the effectiveness of the method, and apply it to study the fetal electrocardiogram signal processing challenge and the two-dimensional random tomography problem.