Robust Dependence Measure using RKHS based Uncertainty Moments and Optimal Transport

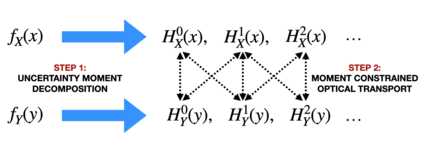
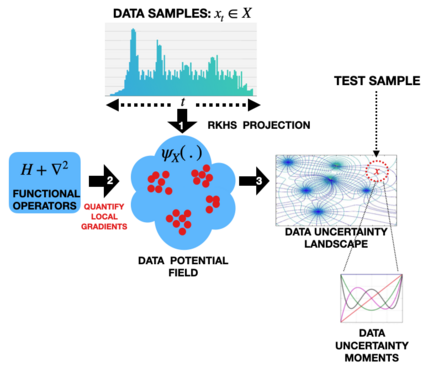
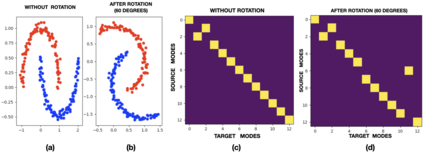
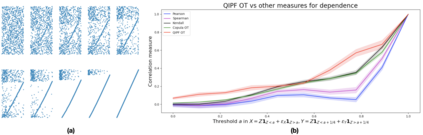
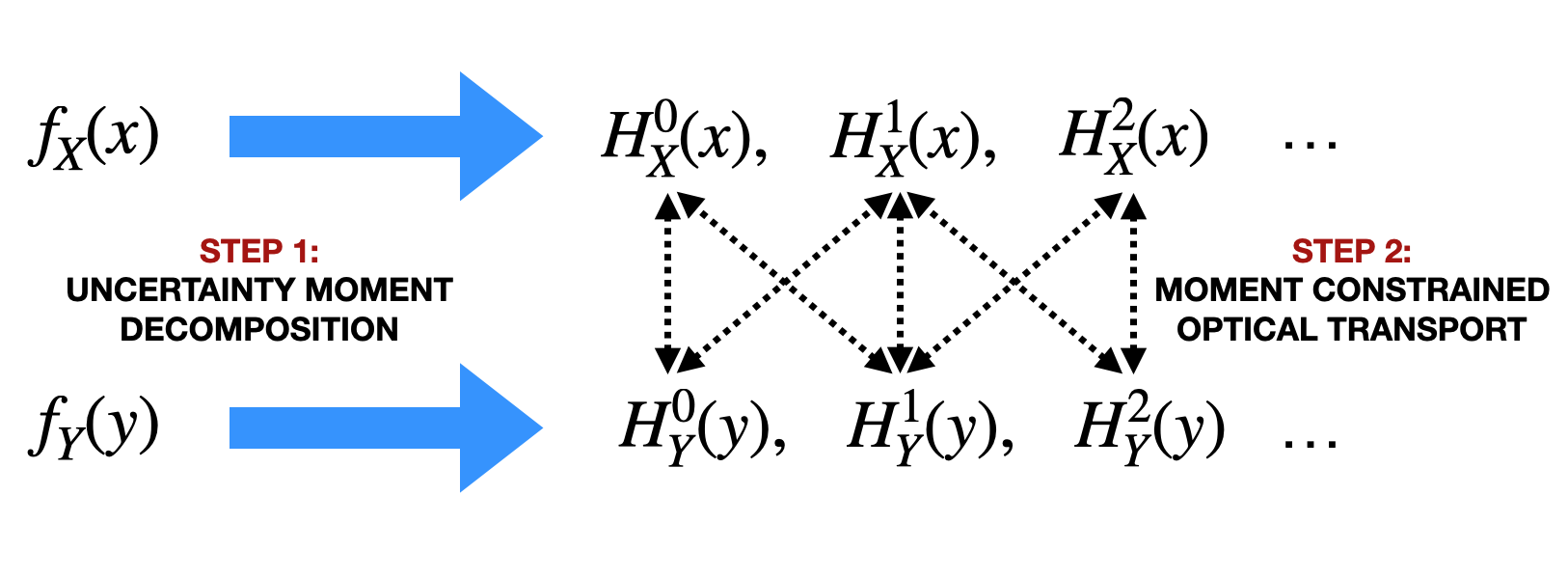
Reliable measurement of dependence between variables is essential in many applications of statistics and machine learning. Current approaches for dependence estimation, especially density-based approaches, lack in precision, robustness and/or interpretability (in terms of the type of dependence being estimated). We propose a two-step approach for dependence quantification between random variables: 1) We first decompose the probability density functions (PDF) of the variables involved in terms of multiple local moments of uncertainty that systematically and precisely identify the different regions of the PDF (with special emphasis on the tail-regions). 2) We then compute an optimal transport map to measure the geometric similarity between the corresponding sets of decomposed local uncertainty moments of the variables. Dependence is then determined by the degree of one-to-one correspondence between the respective uncertainty moments of the variables in the optimal transport map. We utilize a recently introduced Gaussian reproducing kernel Hilbert space (RKHS) based framework for multi-moment uncertainty decomposition of the variables. Being based on the Gaussian RKHS, our approach is robust towards outliers and monotone transformations of data, while the multiple moments of uncertainty provide high resolution and interpretability of the type of dependence being quantified. We support these claims through some preliminary results using simulated data.