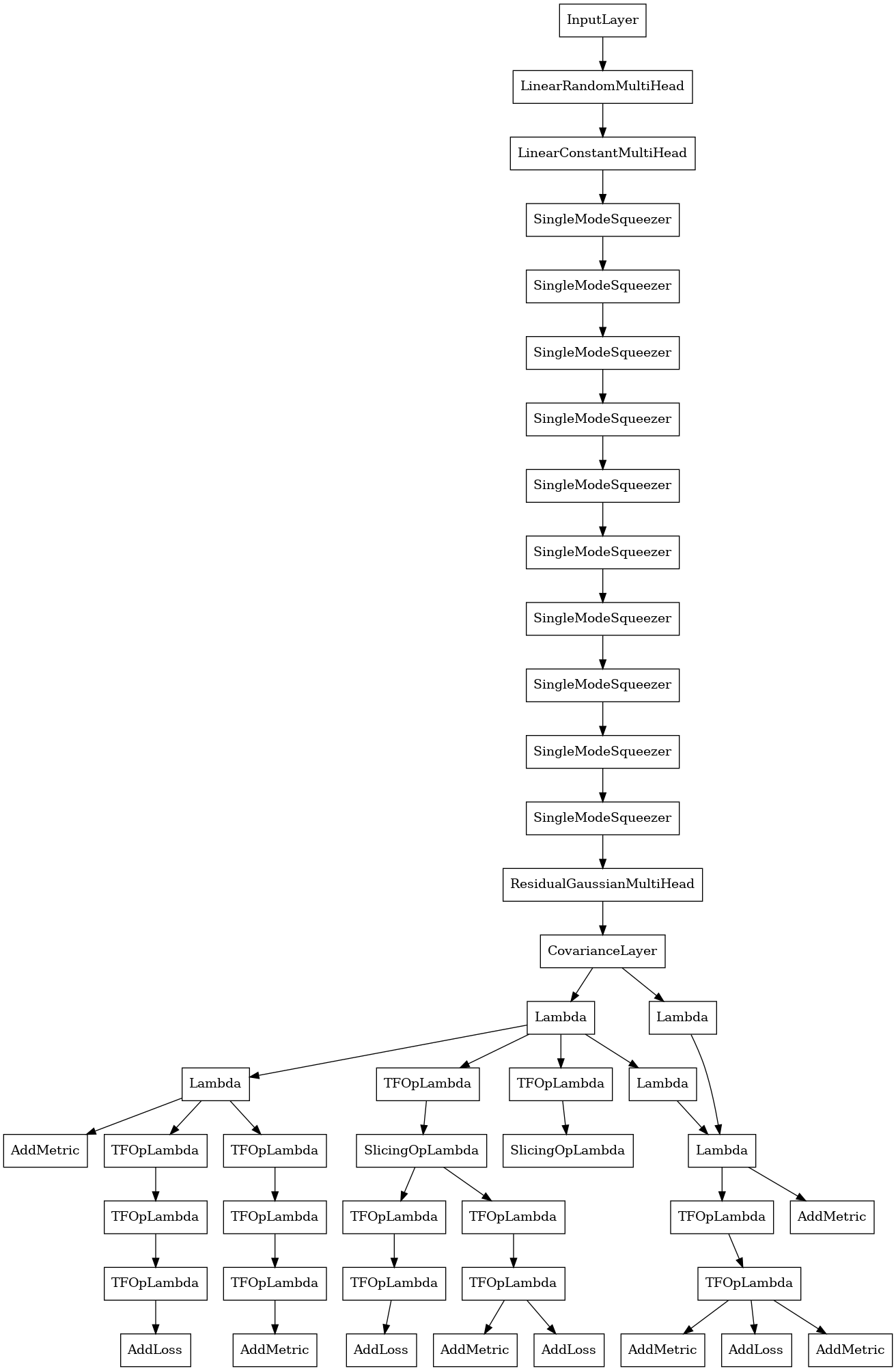
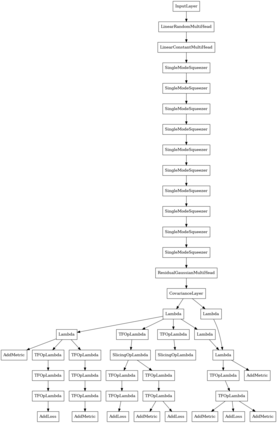
In the context of quantum information, highly nonlinear regimes, such as those supporting solitons, are marginally investigated. We miss general methods for quantum solitons, although they can act as entanglement generators or as self-organized quantum processors. We develop a computational approach that uses a neural network as a variational ansatz for quantum solitons in an array of waveguides. By training the resulting phase-space quantum machine learning model, we find different soliton solutions varying the number of particles and interaction strength. We consider Gaussian states that enable measuring the degree of entanglement and sampling the probability distribution of many-particle events. We also determine the probability of generating particle pairs and unveil that soliton bound states emit correlated pairs. These results may have a role in boson sampling with nonlinear systems and in quantum processors for entangled nonlinear waves.
翻译:在量子信息方面,对高度非线性制度,例如支持索利通的系统,稍有调查。我们错过了量子索利通的一般方法,尽管它们可以作为缠绕生成器或自我组织的量子处理器。我们开发了一种计算方法,利用神经网络作为量子索利通的变异肛门,用于一组波导体中的量子索利通。通过培训由此形成的阶段-空间量子机器学习模型,我们发现不同的单线性解决办法,不同粒子数量和互动强度。我们考虑到高山国家能够测量聚合程度和取样多粒子事件的概率分布。我们还确定生成粒子配对的可能性,并揭开索利顿约束状态的相交配体。这些结果可能在非线性系统的boson采样中发挥作用,在被缠绕的非线性非线性波的量子处理器中发挥作用。