Effects of VLSI Circuit Constraints on Temporal-Coding Multilayer Spiking Neural Networks

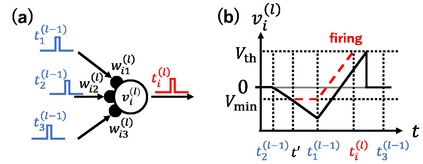
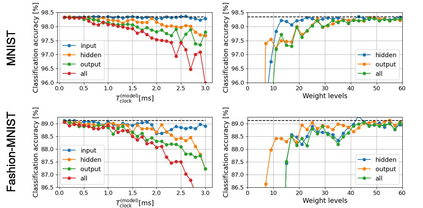
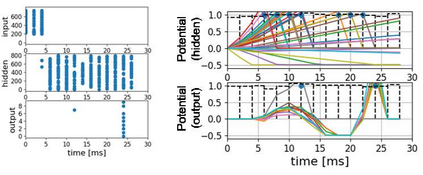
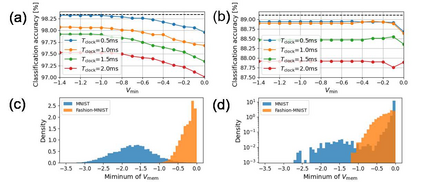
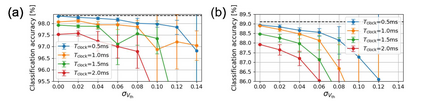
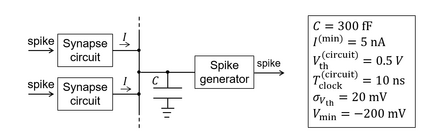
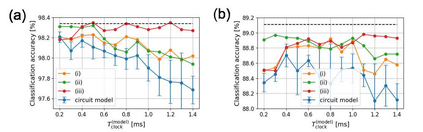
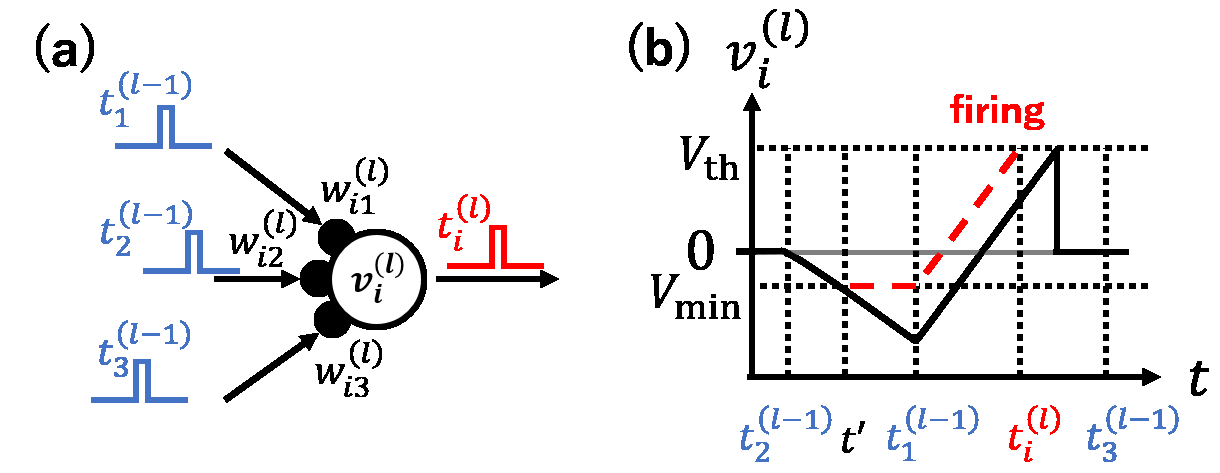
The spiking neural network (SNN) has been attracting considerable attention not only as a mathematical model for the brain, but also as an energy-efficient information processing model for real-world applications. In particular, SNNs based on temporal coding are expected to be much more efficient than those based on rate coding, because the former requires substantially fewer spikes to carry out tasks. As SNNs are continuous-state and continuous-time models, it is favorable to implement them with analog VLSI circuits. However, the construction of the entire system with continuous-time analog circuits would be infeasible when the system size is very large. Therefore, mixed-signal circuits must be employed, and the time discretization and quantization of the synaptic weights are necessary. Moreover, the analog VLSI implementation of SNNs exhibits non-idealities, such as the effects of noise and device mismatches, as well as other constraints arising from the analog circuit operation. In this study, we investigated the effects of the time discretization and/or weight quantization on the performance of SNNs. Furthermore, we elucidated the effects the lower bound of the membrane potentials and the temporal fluctuation of the firing threshold. Finally, we propose an optimal approach for the mapping of mathematical SNN models to analog circuits with discretized time.