Episodic Bandits with Stochastic Experts

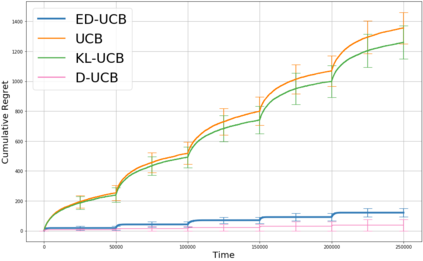
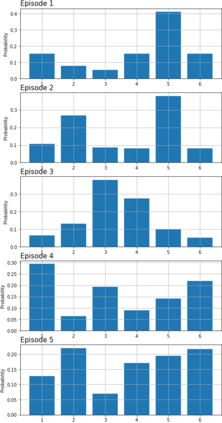
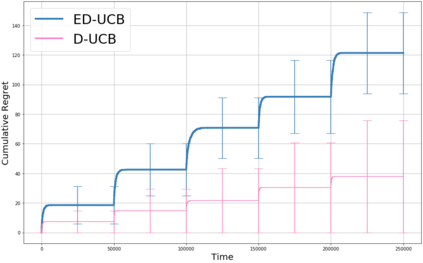
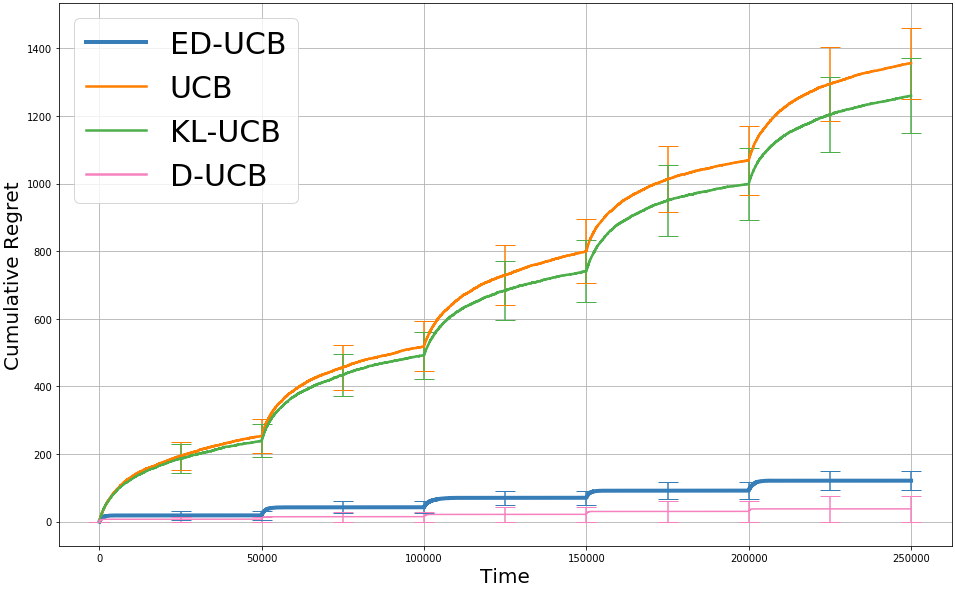
We study a version of the contextual bandit problem where an agent is given soft control of a node in a graph-structured environment through a set of stochastic expert policies. The agent interacts with the environment over episodes, with each episode having different context distributions; this results in the `best expert' changing across episodes. Our goal is to develop an agent that tracks the best expert over episodes. We introduce the Empirical Divergence-based UCB (ED-UCB) algorithm in this setting where the agent does not have any knowledge of the expert policies or changes in context distributions. With mild assumptions, we show that bootstrapping from $\tilde{O}(N\log(NT^2\sqrt{E}))$ samples results in a regret of $\tilde{O}(E(N+1) + \frac{N\sqrt{E}}{T^2})$. If the expert policies are known to the agent a priori, then we can improve the regret to $\tilde{O}(EN)$ without requiring any bootstrapping. Our analysis also tightens pre-existing logarithmic regret bounds to a problem-dependent constant in the non-episodic setting when expert policies are known. We finally empirically validate our findings through simulations.