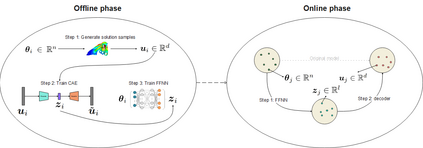
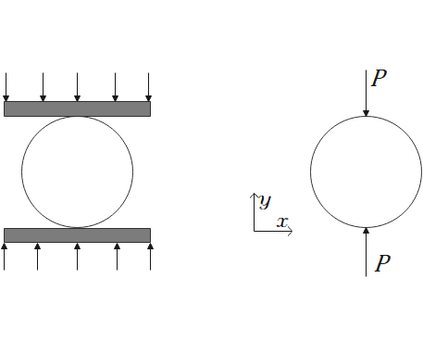
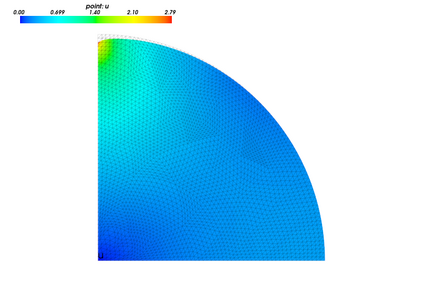
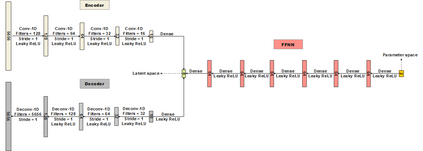
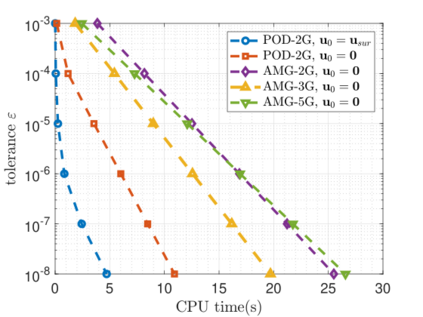
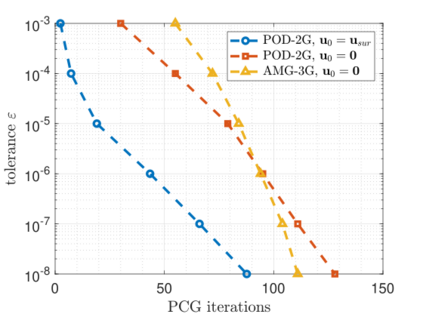
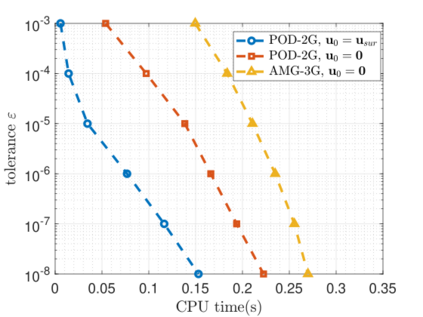
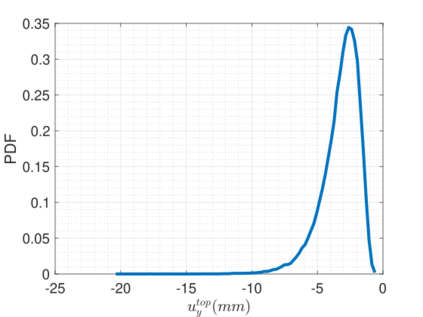
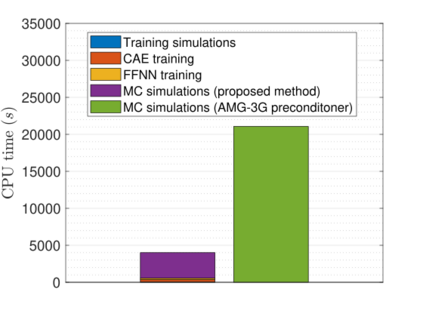
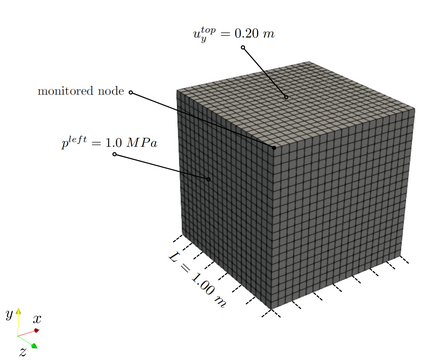
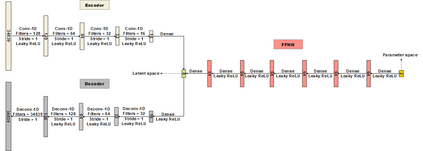
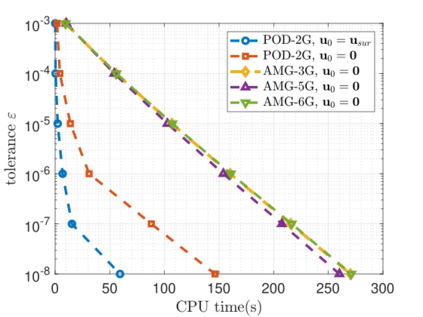
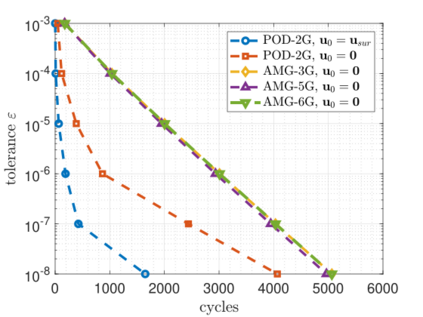
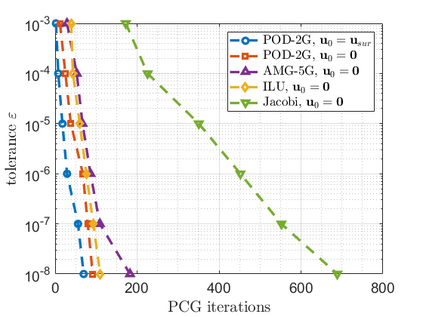
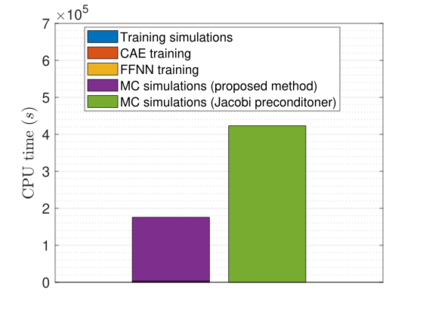
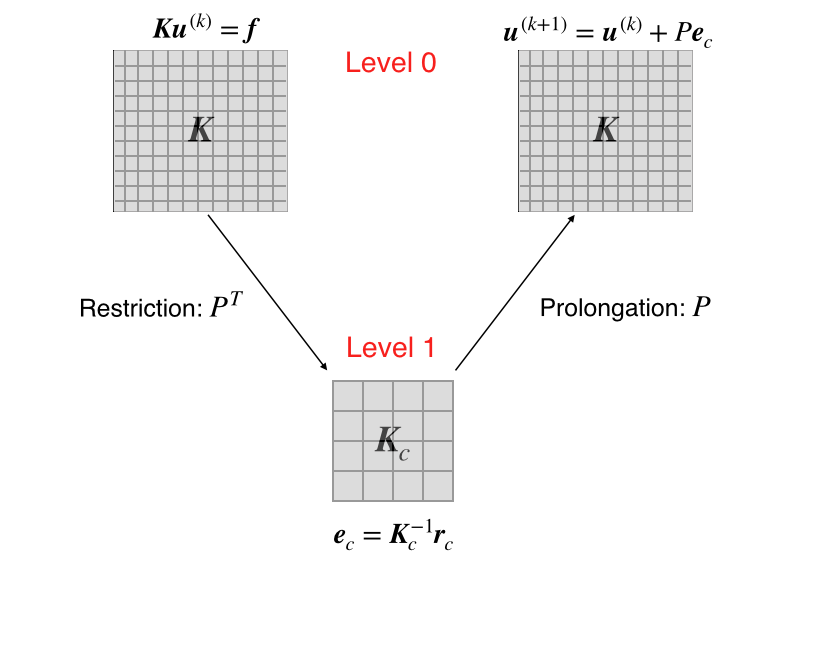
Recent advances in the field of machine learning open a new era in high performance computing. Applications of machine learning algorithms for the development of accurate and cost-efficient surrogates of complex problems have already attracted major attention from scientists. Despite their powerful approximation capabilities, however, surrogates cannot produce the `exact' solution to the problem. To address this issue, this paper exploits up-to-date ML tools and delivers customized iterative solvers of linear equation systems, capable of solving large-scale parametrized problems at any desired level of accuracy. Specifically, the proposed approach consists of the following two steps. At first, a reduced set of model evaluations is performed and the corresponding solutions are used to establish an approximate mapping from the problem's parametric space to its solution space using deep feedforward neural networks and convolutional autoencoders. This mapping serves a means to obtain very accurate initial predictions of the system's response to new query points at negligible computational cost. Subsequently, an iterative solver inspired by the Algebraic Multigrid method in combination with Proper Orthogonal Decomposition, termed POD-2G, is developed that successively refines the initial predictions towards the exact system solutions. The application of POD-2G as a standalone solver or as preconditioner in the context of preconditioned conjugate gradient methods is demonstrated on several numerical examples of large scale systems, with the results indicating its superiority over conventional iterative solution schemes.
翻译:机器学习领域的最新进展开启了一个高性能计算的新时代。应用机器学习算法开发准确和具有成本效益的复杂问题替代物已经引起了科学家的极大关注。尽管他们拥有强大的近似能力,但代孕者无法产生解决问题的“精度”解决办法。为解决这一问题,本文利用最新的ML工具,提供线性方程系统定制的迭代求解器,能够以任何理想的精确度解决大规模不对称问题。具体地说,拟议方法包括以下两个步骤。首先,进行一套较少的模型评估,并使用相应的解决方案,以便利用问题的参数空间到解决问题的空间的大致分布图,使用深的向向向上神经网络提供反馈的深度和向上进化的自动立方形。为了解决这一问题,本文利用最新的ML工具,提供了系统对新查询点的反应的精确初步预测,能够以微不足道的计算成本解决大规模问题。随后,由Algebraic Mulgerid 方法所启发的迭代求解解解解,同时进行以下两个步骤。首先进行一套模型评估,称为POD-2G,然后将一系列的平级前期预测,将一系列常规方法与一系列的平级办法改进,将一系列的平级办法的平比前期推。