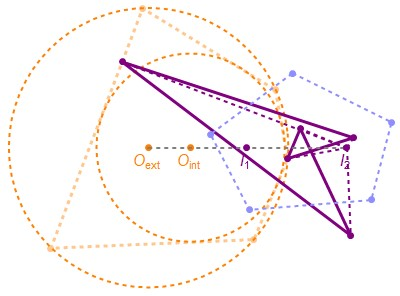
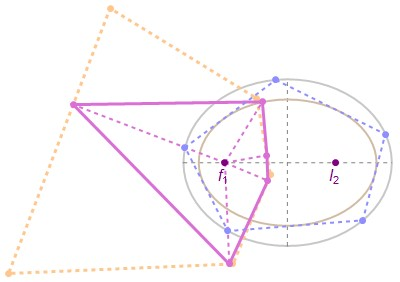
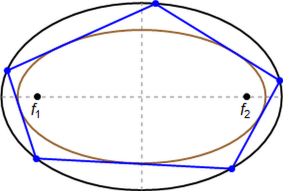
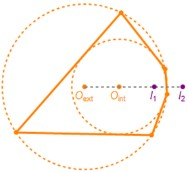
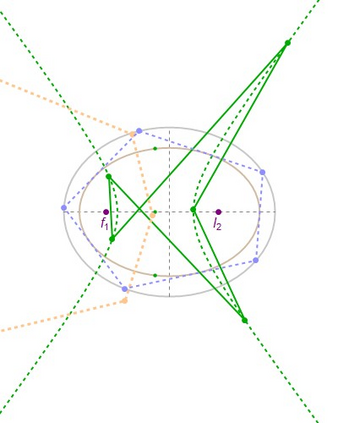
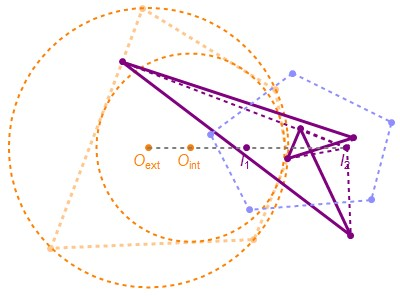
The 1d family of Poncelet polygons interscribed between two circles is known as the Bicentric family. Using elliptic functions and Liouville's theorem, we show (i) that this family has invariant sum of internal angle cosines and (ii) that the pedal polygons with respect to the family's limiting points have invariant perimeter. Interestingly, both (i) and (ii) are also properties of elliptic billiard N-periodics. Furthermore, since the pedal polygons in (ii) are identical to inversions of elliptic billiard N-periodics with respect to a focus-centered circle, an important corollary is that (iii) elliptic billiard focus-inversive N-gons have constant perimeter. Interestingly, these also conserve their sum of cosines (except for the N=4 case).
翻译:Poncelet多边形的1d家族在两个圆圈间相互交织,称为双心族。使用椭圆函数和Liouville的理论,我们显示 (一) 这个家族有内在角共和的内角共振和(二) 有关家庭限制点的踏板多边形有变化性周边。有趣的是, (一) 和 (二) 也是椭圆面圆形N 周期的特性。 此外,由于(二) 中的小圆形多边形与(二) 中小圆面圆形N 的反向偏心圈相同,因此一个重要的必然结果就是 (三) 极圆面圆面圆面的焦点-反向型N形圆形有恒定的周边。 有趣的是, 这些也保存着它们的圆锥形总和( N=4 案例除外 ) 。