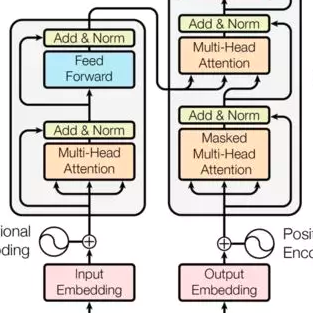
Can we establish provable performance guarantees for transformers? Establishing such theoretical guarantees is a milestone in developing trustworthy generative AI. In this paper, we take a step toward addressing this question by focusing on optimal transport, a fundamental problem at the intersection of combinatorial and continuous optimization. Leveraging the computational power of attention layers, we prove that a transformer with fixed parameters can effectively solve the optimal transport problem in Wasserstein-2 with entropic regularization for an arbitrary number of points. Consequently, the transformer can sort lists of arbitrary sizes up to an approximation factor. Our results rely on an engineered prompt that enables the transformer to implement gradient descent with adaptive stepsizes on the dual optimal transport. Combining the convergence analysis of gradient descent with Sinkhorn dynamics, we establish an explicit approximation bound for optimal transport with transformers, which improves as depth increases. Our findings provide novel insights into the essence of prompt engineering and depth for solving optimal transport. In particular, prompt engineering boosts the algorithmic expressivity of transformers, allowing them implement an optimization method. With increasing depth, transformers can simulate several iterations of gradient descent.
翻译:暂无翻译