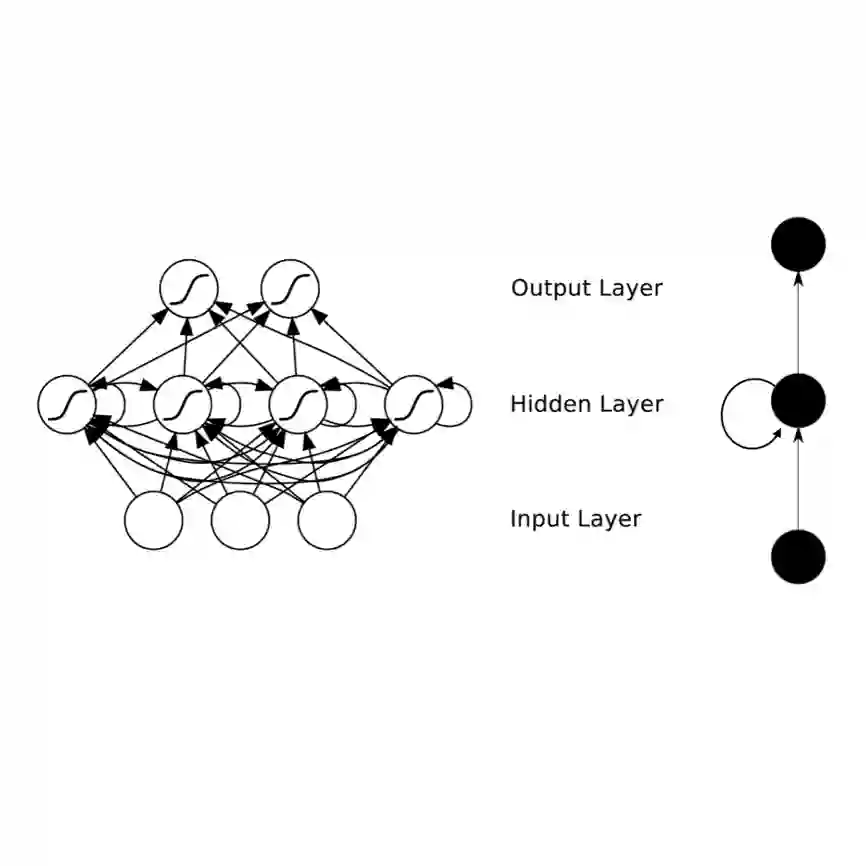
RNNs are popular dynamical models, used for processing sequential data. Prior theoretical work in understanding the properties of RNNs has focused on models with additive interactions, where the input to a unit is a weighted sum of the output of the remaining units in network. However, there is ample evidence that neurons can have gating - i.e. multiplicative - interactions. Such gating interactions have significant effects on the collective dynamics of the network. Furthermore, the best performing RNNs in machine learning have gating interactions. Thus, gating interactions are beneficial for information processing and learning tasks. We develop a dynamical mean-field theory (DMFT) of gating to understand the dynamical regimes produced by gating. Our gated RNN reduces to the classical RNNs in certain limits and is closely related to popular gated models in machine learning. We use random matrix theory (RMT) to analytically characterize the spectrum of the Jacobian and show how gating produces slow modes and marginal stability. Thus, gating is a potential mechanism to implement computations involving line attractor dynamics. The long-time behavior of the gated network is studied using its Lyapunov spectrum, and the DMFT is used to provide an analytical prediction for the maximum Lyapunov exponent. We also show that gating gives rise to a novel, discontinuous transition to chaos, where the proliferation of critical points is decoupled with the appearance of chaotic dynamics; the nature of this chaotic state is characterized in detail. Using the DMFT and RMT, we produce phase diagrams for gated RNN. Finally, we address the gradients by leveraging the adjoint sensitivity framework to develop a DMFT for the gradients. The theory developed here sheds light on the rich dynamical behaviour produced by gating interactions and has implications for architectural choices and learning dynamics.
翻译: RNN 是流行的动态模型, 用于处理序列数据 。 先前用于理解 RNN 特性的理论性工作侧重于具有添加性互动的模型, 单位输入是网络中剩余单元输出的加权和加权。 但是, 有充分的证据表明神经元可以有源化- 即多复制性- 互动。 这种模拟互动对网络的集体动态有重大影响。 此外, 机器学习中表现最佳的 RNN 能够产生慢速模式和边际稳定性。 因此, 模拟互动有利于信息处理和学习任务 。 我们开发了一个动态的动态平均理论( DMFT), 以了解通过加格生成的动态制度。 我们的 GNNNN可以减少到经典 RNNN 的输出。 但是, 我们使用随机矩阵理论来分析网络的频谱。 我们使用LYMMFM 模型来进行快速的变异性分析, 我们使用LYMFD的变异性变异性变异性, 我们使用LYMFD的变异性模型来分析。