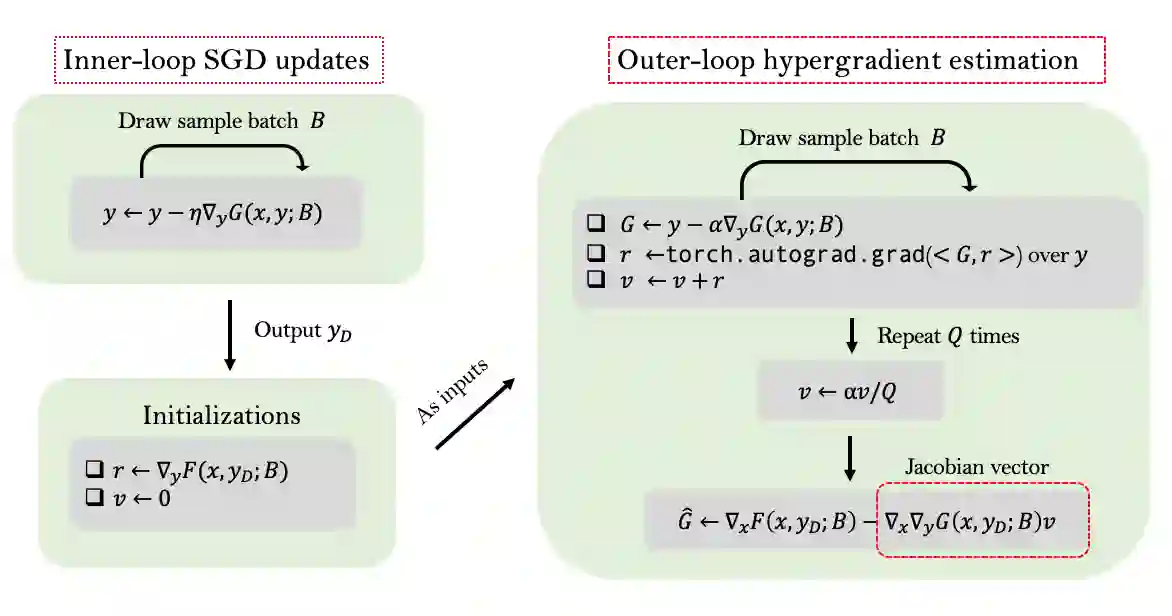
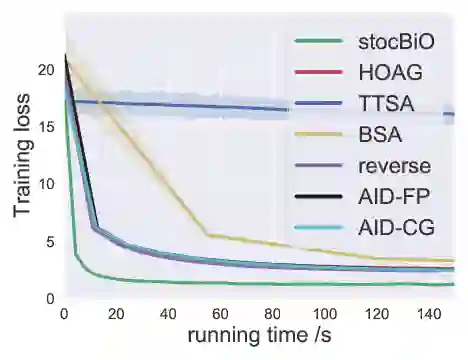
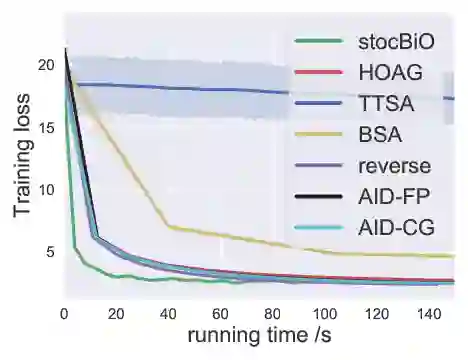
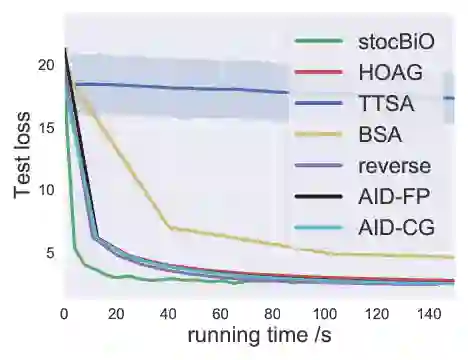
Bilevel optimization has arisen as a powerful tool for many machine learning problems such as meta-learning, hyperparameter optimization, and reinforcement learning. In this paper, we investigate the nonconvex-strongly-convex bilevel optimization problem. For deterministic bilevel optimization, we provide a comprehensive convergence rate analysis for two popular algorithms respectively based on approximate implicit differentiation (AID) and iterative differentiation (ITD). For the AID-based method, we orderwisely improve the previous convergence rate analysis due to a more practical parameter selection as well as a warm start strategy, and for the ITD-based method we establish the first theoretical convergence rate. Our analysis also provides a quantitative comparison between ITD and AID based approaches. For stochastic bilevel optimization, we propose a novel algorithm named stocBiO, which features a sample-efficient hypergradient estimator using efficient Jacobian- and Hessian-vector product computations. We provide the convergence rate guarantee for stocBiO, and show that stocBiO outperforms the best known computational complexities orderwisely with respect to the condition number $\kappa$ and the target accuracy $\epsilon$. We further validate our theoretical results and demonstrate the efficiency of bilevel optimization algorithms by the experiments on meta-learning and hyperparameter optimization.
翻译:双级优化是许多机器学习问题(如元学习、超参数优化和强化学习)的有力工具。在本文件中,我们研究了非convex强调混凝土双级优化问题。对于确定性双级优化,我们根据大致隐含差异(AID)和迭代差异(ITD),分别为两种流行算法提供了全面的趋同率分析。对于基于AID的方法,我们有条不紊地改进了先前的趋同率分析,因为选择了更实际的参数以及一个温暖的启动战略,对于基于 ITD 的方法,我们建立了第一个理论趋同率。我们的分析还提供了一个基于 ITD 和 AID 的双级优化方法之间的定量比较。对于双级优化,我们提出了名为 StocBiO 的新型算法,它使用高效的 Jacobian 和 Hessian- Vector 产品计算方法, 使我们的趋同率率率分析得到改进,我们比O 并且显示,我们比亚公司比亚公司在最高计算精度的精确度和最高计算精确度标准水平上,我们比亚标准的比亚标准的比亚标准化结果。