Fixed-budget online adaptive mesh learning for physics-informed neural networks. Towards parameterized problem inference

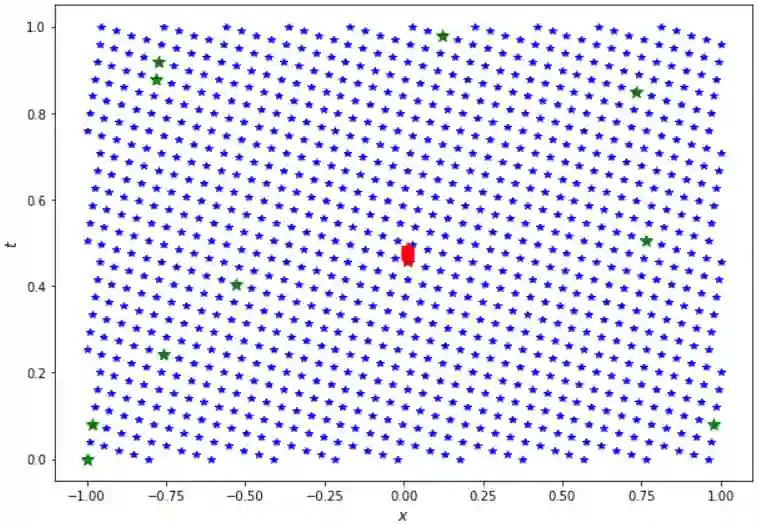
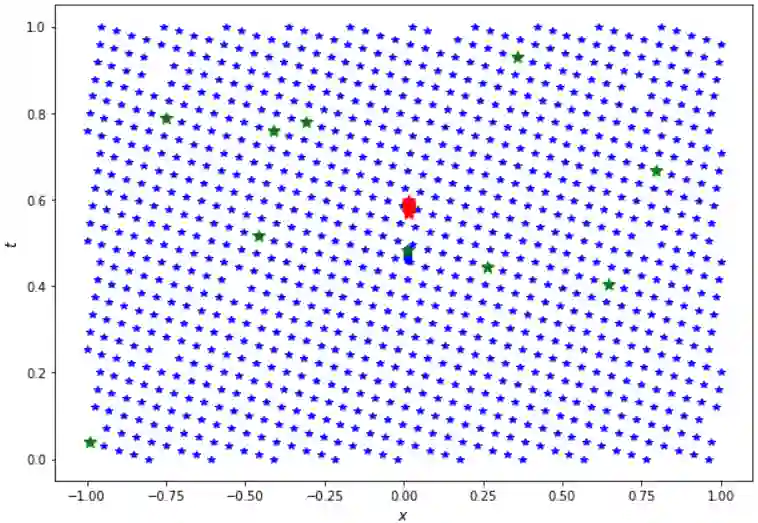
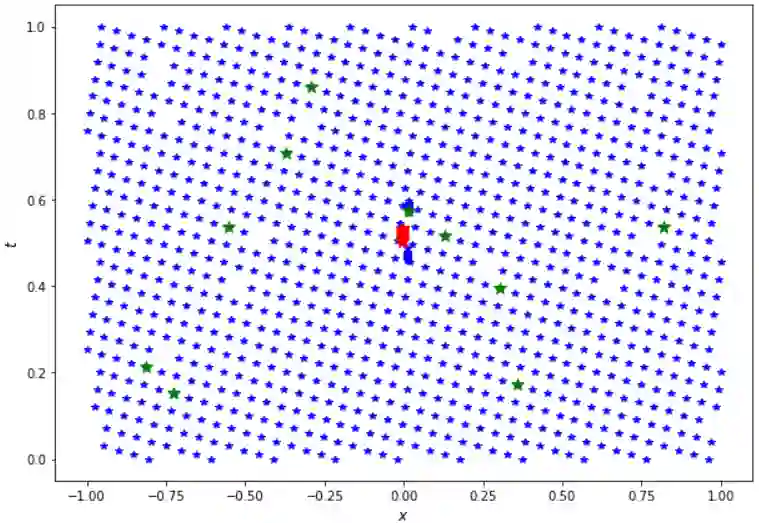
Physics-Informed Neural Networks (PINNs) have gained much attention in various fields of engineering thanks to their capability of incorporating physical laws into the models. PINNs integrate the physical constraints by minimizing the partial differential equations (PDEs) residuals on a set of collocation points. The distribution of these collocation points appears to have a huge impact on the performance of PINNs and the assessment of the sampling methods for these points is still an active topic. In this paper, we propose a Fixed-Budget Online Adaptive Mesh Learning (FBOAML) method, which decomposes the domain into sub-domains, for training collocation points based on local maxima and local minima of the PDEs residuals. The stopping criterion is based on a data set of reference, which leads to an adaptive number of iterations for each specific problem. The effectiveness of FBOAML is demonstrated in the context of non-parameterized and parameterized problems. The impact of the hyper-parameters in FBOAML is investigated in this work. The comparison with other adaptive sampling methods is also illustrated. The numerical results demonstrate important gains in terms of accuracy of PINNs with FBOAML over the classical PINNs with non-adaptive collocation points. We also apply FBOAML in a complex industrial application involving coupling between mechanical and thermal fields. We show that FBOAML is able to identify the high-gradient location and even give better prediction for some physical fields than the classical PINNs with collocation points taken on a pre-adapted finite element mesh.