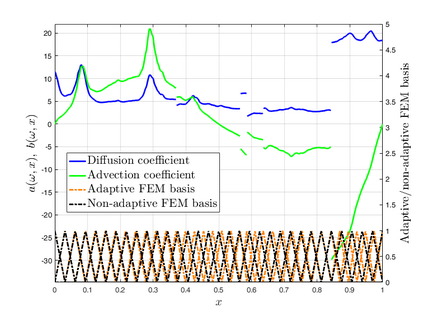
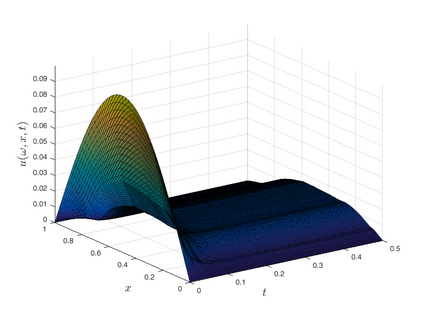
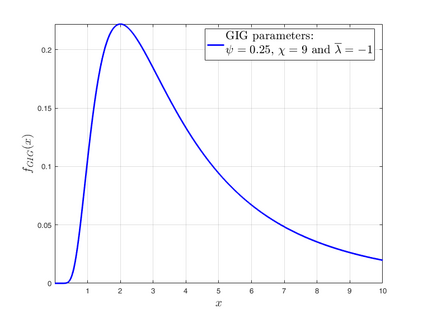
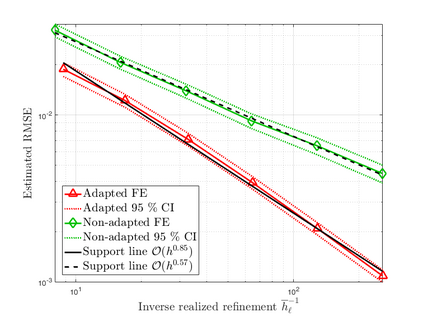
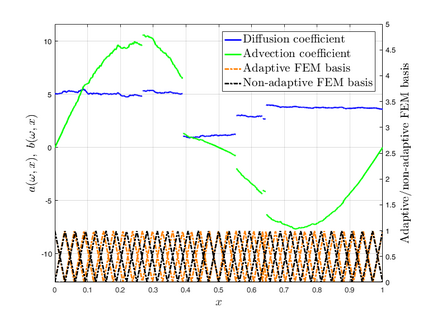
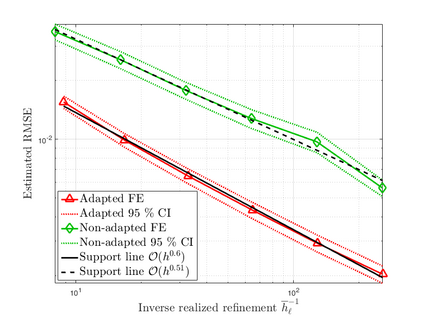
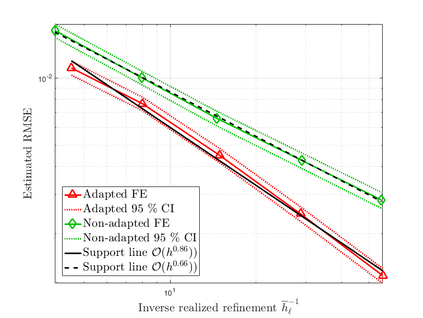
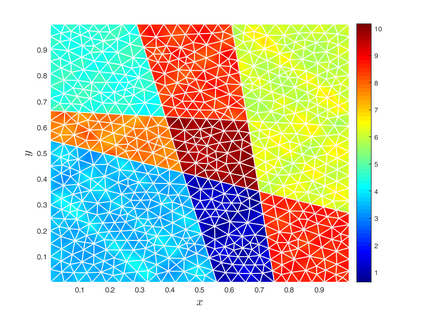
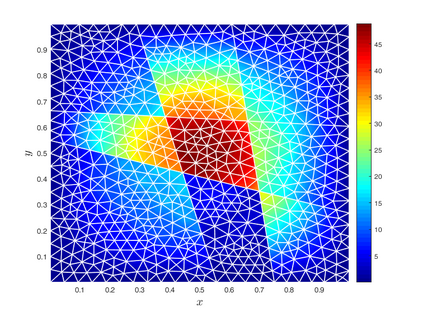
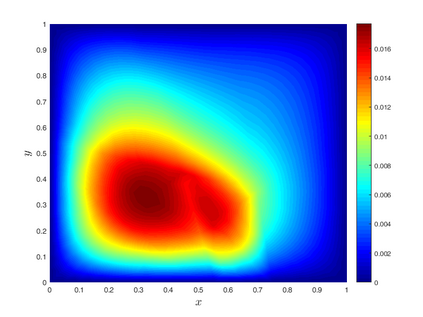
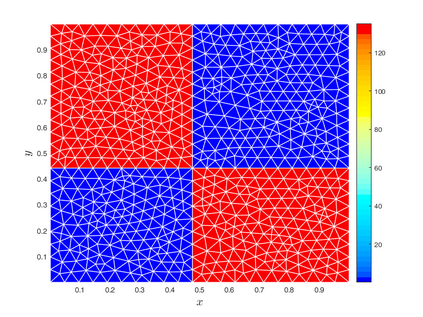
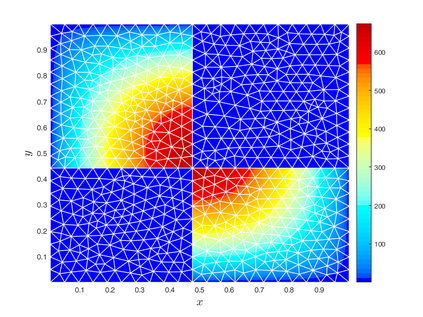
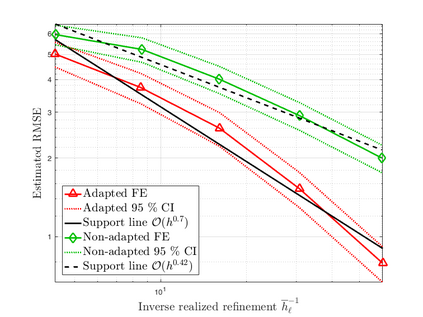
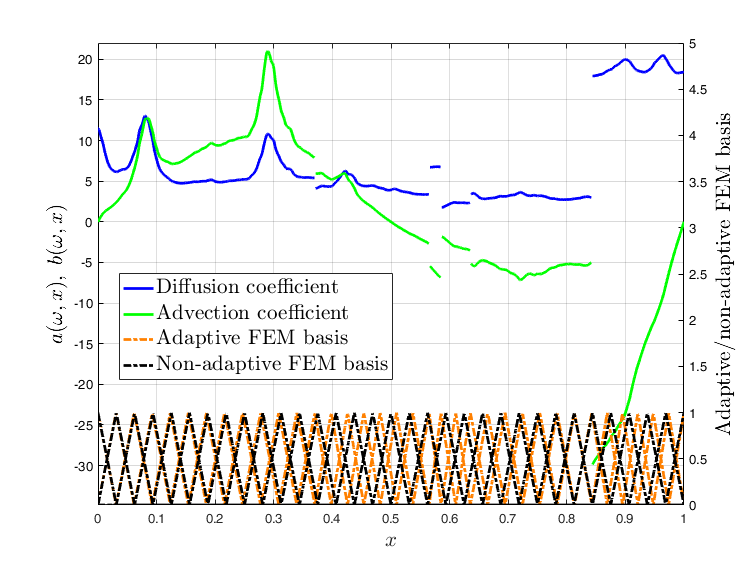
Subsurface flows are commonly modeled by advection-diffusion equations. Insufficient measurements or uncertain material procurement may be accounted for by random coefficients. To represent, for example, transitions in heterogeneous media, the parameters of the equation are spatially discontinuous. Specifically, a scenario with coupled advection- and diffusion coefficients that are modeled as sums of continuous random fields and discontinuous jump components are considered. For the numerical approximation of the solution, an adaptive, pathwise discretization scheme based on a Finite Element approach is introduced. To stabilize the numerical approximation and accelerate convergence, the discrete space-time grid is chosen with respect to the varying discontinuities in each sample of the coefficients, leading to a stochastic formulation of the Galerkin projection and the Finite Element basis.
翻译:地表下流通常以反向扩散方程式为模型; 测量不足或材料采购不确定可按随机系数计算; 例如,为了代表多种介质的过渡,等式参数在空间上不连续; 具体地说,考虑一种假想,配以连续随机字段和不连续跳跃构件的总和为模型的对冲和扩散系数; 对于溶液的数字近似值,采用一个基于一定元素法的适应性、路径性离散方案; 为了稳定数字近似和加速趋同,选择了离散空间时网格,以适应每个系数样本的不同不连续性,从而形成Galerkin预测和Finite Eent基数的随机性配方。