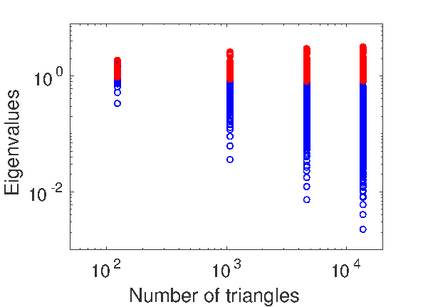
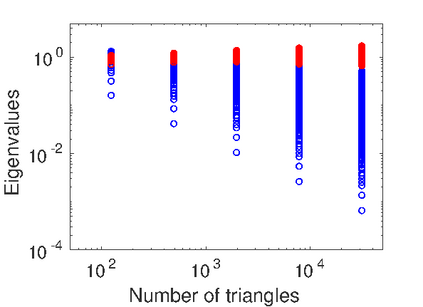
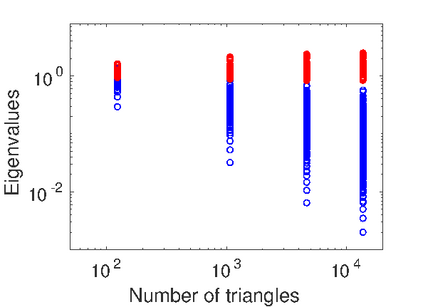
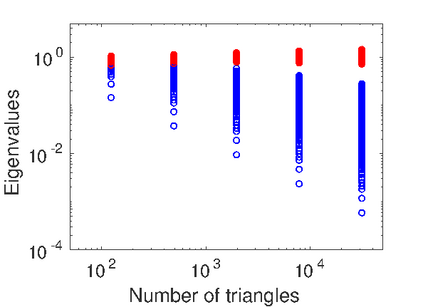
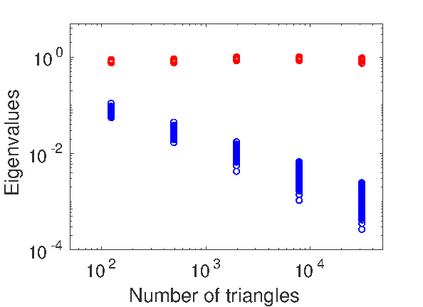
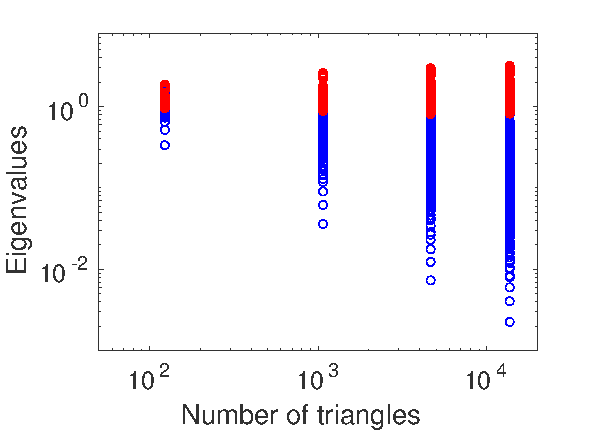
We propose an operator preconditioner for general elliptic pseudodifferential equations in a domain $\Omega$, where $\Omega$ is either in $\mathbb{R}^n$ or in a Riemannian manifold. For linear systems of equations arising from low-order Galerkin discretizations, we obtain condition numbers that are independent of the mesh size and of the choice of bases for test and trial functions. The basic ingredient is a classical formula by Boggio for the fractional Laplacian, which is extended analytically. In the special case of the weakly and hypersingular operators on a line segment or a screen, our approach gives a unified, independent proof for a series of recent results by Hiptmair, Jerez-Hanckes, N\'{e}d\'{e}lec and Urz\'{u}a-Torres. We also study the increasing relevance of the regularity assumptions on the mesh with the order of the operator. Numerical examples validate our theoretical findings and illustrate the performance of the proposed preconditioner on quasi-uniform, graded and adaptively generated meshes.
翻译:我们提出一个操作员的先决条件,用于在域$\Omega$中一般椭圆假相等方程,其中美元为美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=美元=元数=元数=瑞曼元数。对于由低级加列金分解产生的直线方程系统,我们获得独立于网状大小以及测试和试验功能基础选择的条件号。基本成分是Boggio对分数拉平方形的经典公式,该公式在分析中扩展。对于线段或屏幕上的弱和超超超超音速操作员操作员的特殊情况,我们的方法提供了统一、独立的证据,以证明Hiptmair、Jerez-Hankes、N'{e}{e}{e}leclec and Urz\\{u}a-u}a-toristation distrations digraduction and dedustrations.