Age of Coded Updates In Gossip Networks Under Memory and Memoryless Schemes

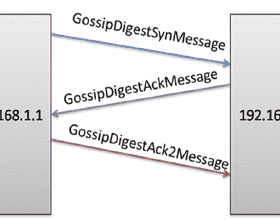
We consider an information update system on a gossip network, where a source node encodes information into $n$ total keys such that any subset of at least $k+1$ keys can fully reconstruct the original information. This encoding process follows the principles of a $k$-out-of-$n$ threshold system. The encoded updates are then disseminated across the network through peer-to-peer communication. We have two different types of nodes in a network: subscriber nodes, which receive a unique key from the source node for every status update instantaneously, and nonsubscriber nodes, which receive a unique key for an update only if the node is selected by the source, and this selection is renewed for each update. For the message structure between nodes, we consider two different schemes: a memory scheme (in which the nodes keep the source's current and previous encrypted messages) and a memoryless scheme (in which the nodes are allowed to only keep the source's current message). We measure the timeliness of information updates by using a recent performance metric, the version age of information. We present explicit formulas for the time average AoI in a scalable homogeneous network as functions of the network parameters under a memoryless scheme. Additionally, we provide strict lower and upper bounds for the time average AoI under a memory scheme.