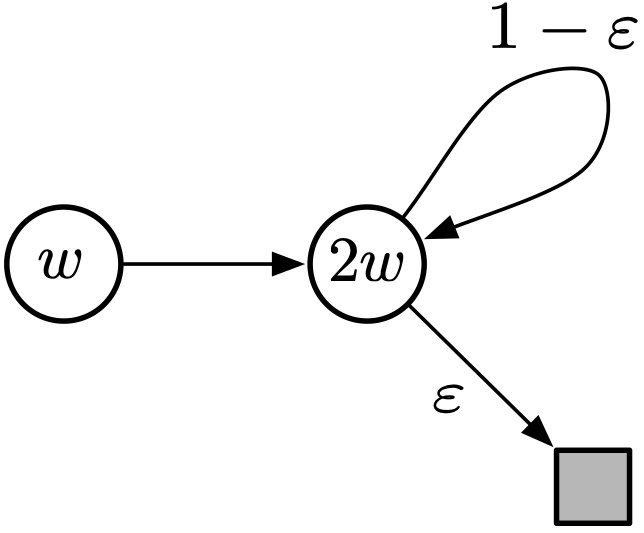
We study the convergence behavior of the celebrated temporal-difference (TD) learning algorithm. By looking at the algorithm through the lens of optimization, we first argue that TD can be viewed as an iterative optimization algorithm where the function to be minimized changes per iteration. By carefully investigating the divergence displayed by TD on a classical counter example, we identify two forces that determine the convergent or divergent behavior of the algorithm. We next formalize our discovery in the linear TD setting with quadratic loss and prove that convergence of TD hinges on the interplay between these two forces. We extend this optimization perspective to prove convergence of TD in a much broader setting than just linear approximation and squared loss. Our results provide a theoretical explanation for the successful application of TD in reinforcement learning.
翻译:暂无翻译