Causal-DRF: Conditional Kernel Treatment Effect Estimation using Distributional Random Forest

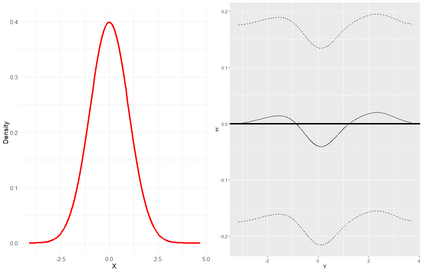
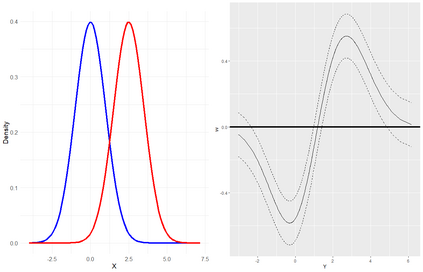
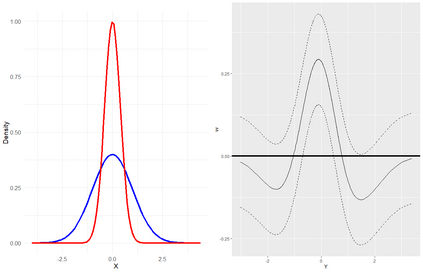
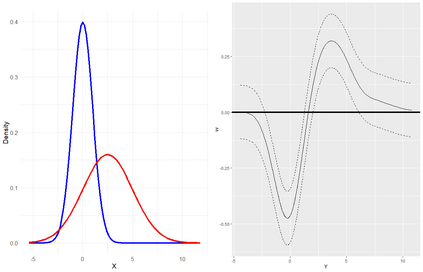
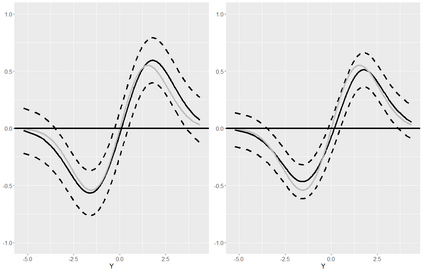
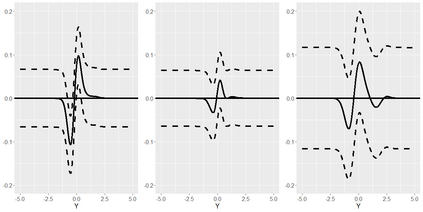
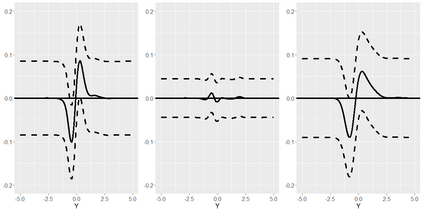
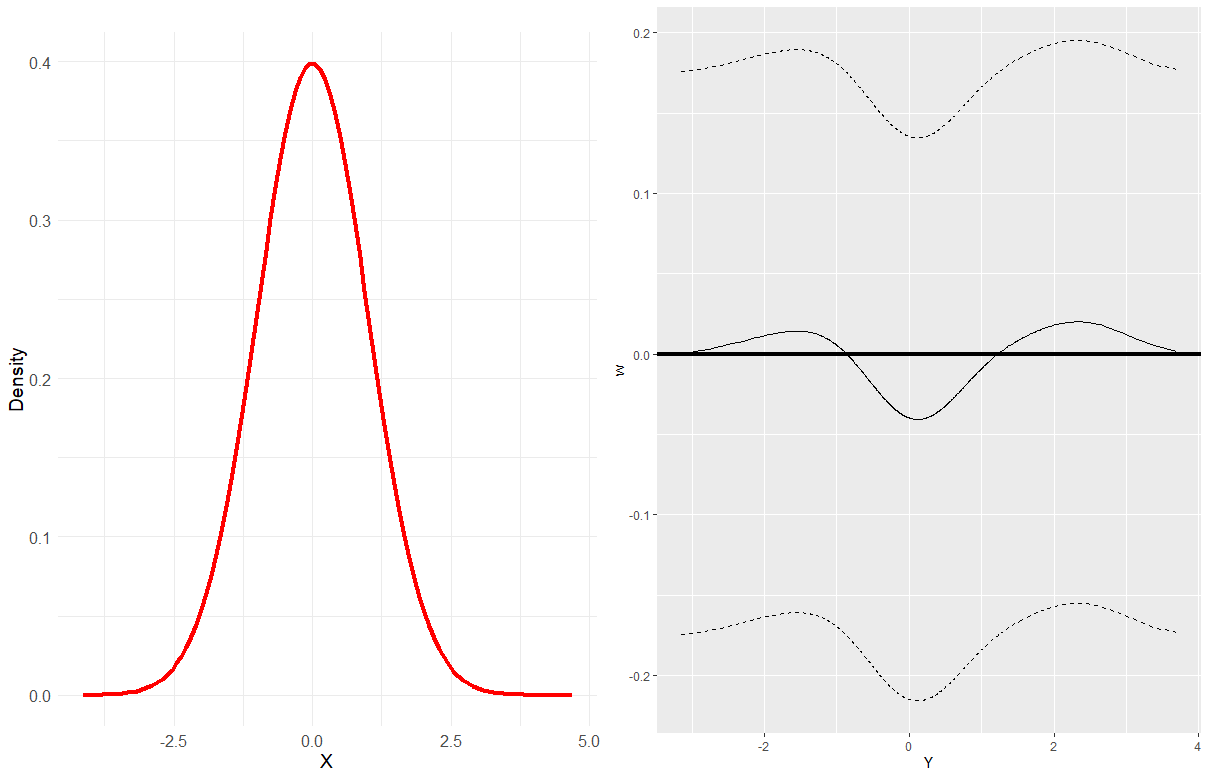
The conditional average treatment effect (CATE) is a commonly targeted statistical parameter for measuring the mean effect of a treatment conditional on covariates. However, the CATE will fail to capture effects of treatments beyond differences in conditional expectations. Inspired by causal forests for CATE estimation, we develop a forest-based method to estimate the conditional kernel treatment effect (CKTE), based on the recently introduced Distributional Random Forest (DRF) algorithm. Adapting the splitting criterion of DRF, we show how one forest fit can be used to obtain a consistent and asymptotically normal estimator of the CKTE, as well as an approximation of its sampling distribution. This allows to study the difference in distribution between control and treatment group and thus yields a more comprehensive understanding of the treatment effect. In particular, this enables the construction of a conditional kernel-based test for distributional effects with provably valid type-I error. We show the effectiveness of the proposed estimator in simulations and apply it to the 1991 Survey of Income and Program Participation (SIPP) pension data to study the effect of 401(k) eligibility on wealth.