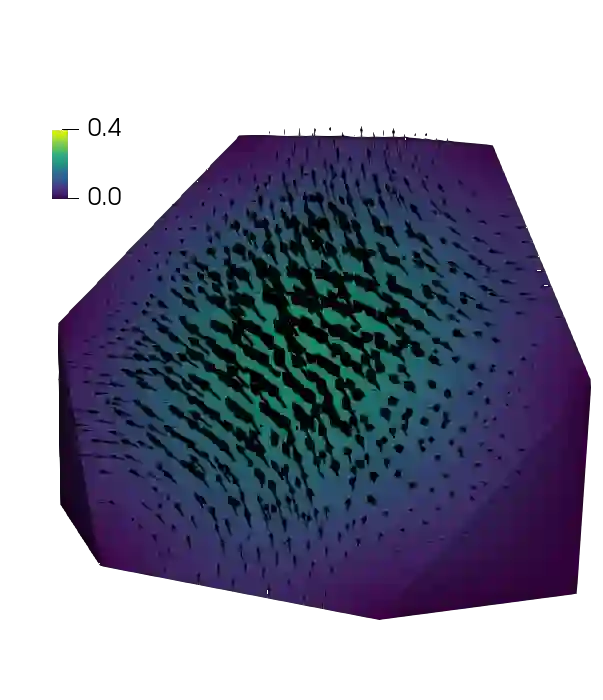
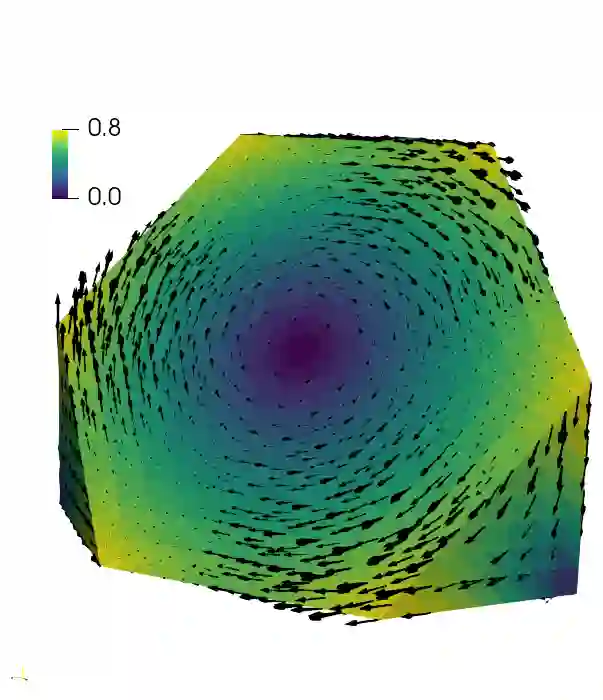
The focus of this study is the construction and numerical validation of parallel block preconditioners for low order virtual element discretizations of the three-dimensional Maxwell equations. The virtual element method (VEM) is a recent technology for the numerical approximation of partial differential equations (PDEs), that generalizes finite elements to polytopal computational grids. So far, VEM has been extended to several problems described by PDEs, and recently also to the time-dependent Maxwell equations. When the time discretization of PDEs is performed implicitly, at each time-step a large-scale and ill-conditioned linear system must be solved, that, in case of Maxwell equations, is particularly challenging, because of the presence of both H(div) and H(curl) discretization spaces. We propose here a parallel preconditioner, that exploits the Schur complement block factorization of the linear system matrix and consists of a Jacobi preconditioner for the H(div) block and an auxiliary space preconditioner for the H(curl) block. Several parallel numerical tests have been perfomed to study the robustness of the solver with respect to mesh refinement, shape of polyhedral elements, time step size and the VEM stabilization parameter.
翻译:本研究的重点是为三维最大韦尔方程式的低顺序虚拟离散性虚拟元件的平行区块先决条件的构建和数字验证。虚拟元件方法(VEM)是部分差分方程(PDEs)数字近似值的最新技术,该技术将有限元素一般化为多式计算网格。到目前为止,VEM已扩大到PDEs描述的一些问题,最近还扩大到基于时间的Maxwell方程式。当PDEs的时间分解在每一个时间阶段都必须隐含地进行时分解时,一个大型和不完善的线性系统必须得到解决时,在最大韦尔方程式的情况下,由于存在H(div)和H(cur)离异性方程式,这特别具有挑战性。我们在此提议一个平行的前提条件,即利用Schur对线性系统矩阵的区块因子化作用,由H(div)区块和H(curl)区块的辅助空间先决条件组成。一些平行的数字测试已经进行,以研究溶性度、稳定度和稳定度的磁度等度的大小。